Lançamento Horizontal e Oblíquo 10 Exercícios

Questão 01 sobre Lançamento Horizontal e Oblíquo: (Aman) Uma esfera é lançada com velocidade horizontal constante de módulo v = 5 m/s da borda de uma mesa horizontal. Ela atinge o solo num ponto situado a 5 m do pé da mesa conforme o desenho abaixo.

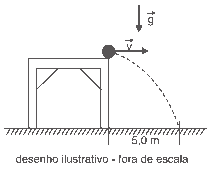
Desprezando a resistência do ar, o módulo da velocidade com que a esfera atinge o solo é de: Dado: Aceleração da gravidade: g=10 m/s2

a) 4 m/s
b) 5 m/s
c) 5 √2 m/s
d) 6 √2 m/s
e) 5 √2 m/s

Questão 02. (Uerj) Três blocos de mesmo volume, mas de materiais e de massas diferentes, são lançados obliquamente para o alto, de um mesmo ponto do solo, na mesma direção e sentido e com a mesma velocidade.

Observe as informações da tabela:

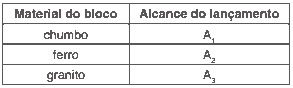
A relação entre os alcances A1, A2 e A3 está apresentada em:
a) A1 > A2 > A3
b) A1 < A2 < A3
c) A1 = A2 > A3
d) A1 = A2 = A3

Questão 03. (Pucrj) Um projétil é lançado com uma velocidade escalar inicial de 20 m/s com uma inclinação de 30° com a horizontal, estando inicialmente a uma altura de 5,0 m em relação ao solo. A altura máxima que o projétil atinge, em relação ao solo, medida em metros, é:

Considere a aceleração da gravidade g = 10 m/s2
a) 5,0
b) 10
c) 15
d) 20
e) 25

Questão 04 sobre Lançamento Horizontal e Oblíquo: (Ucs) Uma noiva, após a celebração do casamento, tinha de jogar o buquê para as convidadas. Como havia muitas ex-namoradas do noivo, ela fazia questão de que sua melhor amiga o pegasse. Antes de se virar para, de costas, fazer o arremesso do buquê, a noiva, que possuía conhecimento sobre movimento balístico, calculou a que distância aproximada a amiga estava dela: 5,7 m. Então ela jogou o buquê, tomando o cuidado para que a direção de lançamento fizesse um ângulo de 60° com a horizontal. Se o tempo que o buquê levou para atingir a altura máxima foi de 0,7 s, qual o valor aproximado da velocidade dele ao sair da mão da  noiva? (Despreze o atrito com o ar.

Considere a aceleração da gravidade igual a 10 m/s2, cos 60° = 0,5 e sen 60° = 0,87.)
a) 1,5 m/s
b) 5,5 m/s
c) 6,0 m/s
d) 8,0 m/s
e) 11,0 m/s

TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:

Três bolas − X, Y e Z − são lançadas da borda de uma mesa, com velocidades iniciais paralelas ao solo e mesma direção e sentido. A tabela abaixo mostra as magnitudes das massas e das velocidades iniciais das bolas.

Questão 05. (Uerj) As relações entre os respectivos tempos de queda tx, ty e tz das bolas X, Y e Z estão apresentadas em:

a) tx < ty < tz
b) ty < tz < tx
c) tz < ty < tx
d) ty = tx = tz

Questão 06. (Uerj) As relações entre os respectivos alcances horizontais Ax, Ay e Az das bolas X, Y e Z, com relação à borda da mesa, estão apresentadas em:

a) Ax < Ay < Az
b) Ay = Ax < A z
c) Az < Ay < Ax
d) Ay < Az < Ax

Questão 07 sobre Lançamento Horizontal e Oblíquo: (Uff) Após um ataque frustrado do time adversário, o goleiro se prepara para lançar a bola e armar um contra-ataque. Para dificultar a recuperação da defesa adversária, a bola deve chegar aos pés de um atacante no menor tempo possível. O goleiro vai chutar a bola, imprimindo sempre a mesma velocidade, e deve controlar apenas o ângulo de lançamento. A figura mostra as duas trajetórias possíveis da bola num certo momento da partida.

Assinale a alternativa que expressa se é possível ou não determinar qual destes dois jogadores receberia a bola no menor tempo. Despreze o efeito da resistência do ar.

a) Sim, é possível, e o jogador mais próximo receberia a bola no menor tempo.

b) Sim, é possível, e o jogador mais distante receberia a bola no menor tempo.

c) Os dois jogadores receberiam a bola em tempos iguais.

d) Não, pois é necessário conhecer os valores da velocidade inicial e dos ângulos de lançamento.

e) Não, pois é necessário conhecer o valor da velocidade inicial.

Questão 08. (Ufu) Uma pedra é lançada do solo com velocidade de 36 km/h fazendo um ângulo de 45° com a horizontal. Considerando g = 10 m/s² e desprezando a resistência do ar, analise as afirmações abaixo.

I. A pedra atinge a altura máxima de 2,5 m.
II. A pedra retorna ao solo ao percorrer a distância de 10 m na horizontal.
III. No ponto mais alto da trajetória, a componente horizontal da velocidade é nula.

Usando as informações do enunciado, assinale a alternativa correta.
a) Apenas I é verdadeira.
b) Apenas I e II são verdadeiras.
c) Apenas II e III são verdadeiras.
d) Apenas II é verdadeira.

Questão 09.(Uesc) Galileu, ao estudar problemas relativos a um movimento composto, propôs o princípio da independência dos movimentos simultâneos — um móvel que descreve um movimento composto, cada um dos movimentos componentes se realiza como se os demais não existissem e no mesmo intervalo de tempo.

Assim, considere um corpo lançado obliquamente a partir do solo sob ângulo de tiro de 45° e com velocidade de módulo igual a 10,0 m/s. Desprezando-se a resistência do ar, admitindo-se que o módulo da aceleração da gravidade local é igual a 10 m/s2 e sabendo-se que cos 45° = , e sen 45° = é correto afirmar:

a) O alcance do lançamento é igual a 5,0 m.
b) O tempo total do movimento é igual a √2s .
c) A altura máxima atingida pelo corpo é igual a 10,0 m.
d) O corpo atinge a altura máxima com velocidade nula.
e) A velocidade escalar mínima do movimento é igual a 10,0 m/s.

Questão 10 sobre Lançamento Horizontal e Oblíquo: (Puccamp) Do alto de uma montanha em Marte, na altura de 740 m em relação ao solo horizontal, é atirada horizontalmente uma pequena esfera de aço com velocidade de 30 m/s. Na superfície deste planeta a aceleração gravitacional é de 3,7 m/s2.

A partir da vertical do ponto de lançamento, a esfera toca o solo numa distância de, em metros,
a) 100
b) 200
c) 300
d) 450
e) 600

🔵 >>> Verifique todos os nossos exercícios e atividades de Física.

Gabarito com as respostas da lista com 10 exercícios de física sobre Lançamento Horizontal e Oblíquo:

01. e;
02. d;
03. b;
04. d;
05. d;

06. c;
07. b;
08. b;
09. b;
10. e

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína