10 Exercícios sobre Sistemas de Duas Equações do Segundo Grau para o 9° Ano com Gabarito

Lista com 10 atividades de Matemática sobre Sistemas de Duas Equações do Segundo Grau para o 9º Ano do Ensino Fundamental com Gabarito!

ATENÇÃO!!! O Gabarito encontra-se no final da página!!!

Questão 01. Em uma fração equivalente a 3/2, a diferença entre os quadrados dos seus termos é 80. Qual é essa fração?

Questão 02. Considere dois números reais positivos x e y. Se você dividir x por y, encontrará 3 como resultado. Sabendo que o quadrado do número y é igual ao número x aumentado de 10 unidades, quais são esses números?

Questão 03 com Exercícios sobre Sistemas de Duas Equações do Segundo Grau para o 9° Ano: (CEFET/AL02) Uma partícula move-se sobre uma reta e sua posição no instante x é dada pela função y = x² – 5x – 38. Em qual dos instantes abaixo, a partícula encontra-se na posição y = 12?

a) x = 6
b) x = 7
c) x = 8
d) x = 9
e) x = 10

Questão 04. Considere o sistema de equações

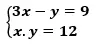
e determine os valores de x e y que são soluções desse sistema.

Questão 05. Determine dois números inteiros e positivos tais que o produto entre eles seja 140, e a diferença entre eles seja 4.

Questão 06. Resolvas os sistemas de equações abaixo:

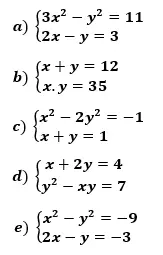
Questão 07. A diferença entre dois números inteiros positivos é igual a 3. O quadrado do números maior menos o dobro do número menor é 86. Quais são esses números?

Questão 08. Um dos pares ordenados ( x, y) que é solução do sistema

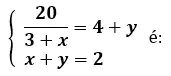
Questão 09. (CEFET/AL04) Encontre o valor de c de modo que 2, seja solução da equação x² – 3x + c = 0:

a) 0
b) 10
c) 2
d) – 4
e) 8

Questão 10. Multiplicando x por y vamos obter 80 e dividindo x por y , obtemos 5. Nessas condições determine os números x e y.

Gabarito com as respostas dos Exercícios sobre Sistemas de Duas Equações do Segundo Grau para o 9° Ano do ensino fundamental:

01. 12/8

02. x = 15 e y = 5

x/y = 3 x = 3 y substituindo em y² = x + 10
Temos: y² = 3y + 10
y² – 3y – 10 = 0 a = 1 b = – 3 c = -10

Δ = b² – 4.a.c
Δ = (-3)² – 4.1.(-10)
Δ = 9 + 40
Δ = 49

y = 3 ± 7)/2
y’ = 10/2 y” = – 4/2
y’ = 5 y” = – 2 não serve
quando y = 5 x = 3y x = 3.5 x = 15

03. E

y = x² – 5x – 38
12 = x² – 5x – 38
x² – 5x – 38 – 12 = 0
x² – 5x – 50 = 0

Δ = b² – 4.a.c
Δ = (-5)² – 4.1.(-50)
Δ = 25 + 200
Δ = 225

x = (- b ± √Δ)/2.a
x = 5 ± √225)/2.1
x = (5 ± 15)/2
x’ = (5 + 15)/2 x” = (5 – 15)/2
x’ = 10 x” = – 5 Não serve

04. x = 4 e y = 3 ou x = -1 e y = -12

05. 14 e 10

x – y = 4 x = 4 + y substituindo em x . y = 140
Temos: (4 + y ).y = 140
4y + y² = 140
y² + 4y – 140 = 0 a = 1 b = 4 c = – 140

Δ = b² – 4.a.c
Δ = 4² – 4.1.(-140)
Δ = 16 + 560
Δ = 576

y = (-4 ± 24)/2
y’ = 20/2 y” = – 28/2
y’ = 10 y” = -14 não serve
quando y =10 x = 4 + 10 x = 14

06. a) ( 2,1)
b) x = 7 e y = 5 ou x = 5 e y = 7
c) (6,5);(-2,3)
d) (6,-1);(-2/3,7/3)
e) (-4,-5): (0,3)

07. 10 e 7;
08. D;
09. C;

X = 2
x² – 3x + c = 0
2² – 3.2 + c = 0
4 – 6 + c = 0
– 2 + c = 0
c = 2

10. x . y = 80
x : y = 5 x = 5y x .y = 80
5y.y = 80
5y² = 80
y² = 80/5
y² = 16
y = ± √16
y = 4 ou y – 4

x = 5y ou x = 5y
x = 5 . 4 x = 5.(-4)
x = 20 x = – 20

x = 20 e y = 4 ou x = – 20 e y = – 4

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína