Exercícios sobre Polinômios na Forma Reduzida para o 8° Ano com Gabarito

Lista com 15 atividades de Matemática sobre Polinômios na Forma Reduzida para o 8º Ano do Ensino Fundamental com Gabarito!

ATENÇÃO!!! O Gabarito encontra-se no final da página!!!

Questão 01. 3a – [ – 5b + 8c – ( a + 3b + 5c ) – ( b + c ) ] – 2a

Questão 02. 3a³ – 2a + 5a³ – 4a³ – 3a

Questão 03. Qual é o polinômio que representa o perímetro da figura seguinte?

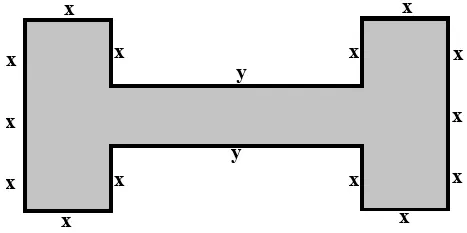
Questão 04. ax – [ – 2bx – ( ab + ax – bx ) + 2ab ] – ( 2ax – ab )

Questão 05. 3a + 8ab + 5b – 2ab – 7a + b – ab

Questão 06. A figura é um retângulo cujas medidas estão indicadas. Nessas condições:

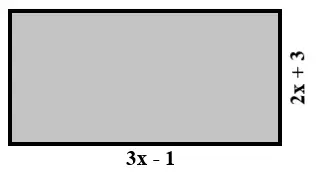
a) Qual é o polinômio reduzido que representa o perímetro desse retângulo?

b) Qual é o perímetro desse retângulo quando x = 6,5 cm?

Questão 07. 7x² – 6x + 9 + 2x – 5x² – 8

Questão 08. Escreva o polinômio que representa a área:

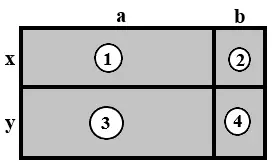
a) do retângulo 1. ax
b) do retângulo 2. bx
c) do retângulo 3. ay
d) do retângulo 4. by
e) da figura toda. ax + bx + ay + by

Questão 09 com Exercícios sobre Polinômios na Forma Reduzida para o 8° Ano: Escreva o polinômio que representa:

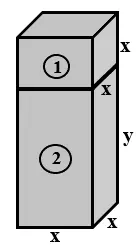
a) o volume do sólido 1. x³
b) o volume do sólido 2. x²y
c) o volume do sólido todo. x³ + x²y

Questão 10. Escreva o polinômio 2r + ( – s + rs ) – ( r + 3rs – 5s ) e determine o seu valor numérico para r = 2, s = – 2.

Questão 11. ab – ( – 2a + b ) – ( c + 3a – ab ) + ( 4a – c )

Questão 12. 2xy + 1xy²/2 – 2x²y/3 – xy² + 1xy/4 + 1x²y/6

Questão 13. 8x³ – ( x² + 7x – 5 ) + ( – 2x³ + 6x² – x ) – ( – 1 + 3x )

Questão 14. Escreva o polinômio que representa a área:

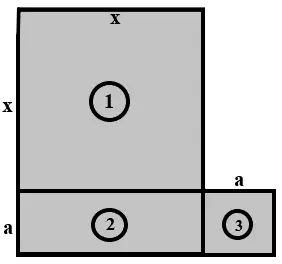
a) da figura 1 . x²
b) da figura 2. ax
c) da figura 3. a²
d) da figura toda. x² + ax + a²

Questão 15. x – ( – 5y + 3x ) + ( xy – x – y ) – ( 7y + 2xy )

Gabarito com as respostas dos Exercícios sobre Polinômios na Forma Reduzida para o 8° Ano do ensino fundamental:

01. 3a – [ – 5b + 8c – ( a + 3b + 5c ) – ( b + c ) ] – 2a
3a – [ – 5b + 8c – a – 3b – 5c – b – c ] – 2a =
3a + 5b – 8c + a + 3b + 5c + b + c – 2a =
3a + a – 2a + 5b + 3b + b – 8c + 5c + c =
2a + 9b – 2c

02. 3a³ + 5a³ – 4a³ – 2a – 3a =
8a³ – 4a³ – 5a =
4a³ – 5a

03. 14x + 2y

04. ax – [ – 2bx – ( ab + ax – bx ) + 2ab ] – ( 2ax – ab )
ax – [ – 2bx – ab – ax + bx + 2ab ] – 2ax + ab =
ax + 2bx + ab + ax – bx – 2ab – 2ax + ab =
ax + ax – 2ax + ab + ab – 2ab+ 2bx – bx =
bx

05. 3a + 8ab + 5b – 2ab – 7a + b – ab
3a – 7a + 8ab – ab + 5b + b =
– 4a + 7ab + 6b

06. a) 2(3x – 1 ) + 2 ( 2x + 3 ) =
6x – 2 + 4x + 6 =
6x + 4x – 2 + 6 =
10x + 4

b) 10x + 4 =
10 . (6,5) + 4 =
65 + 4 =
69 cm

07. 7x² – 6x + 9 + 2x – 5x² – 8
7x² – 5x² – 6x + 2x + 9 – 8 =
7x² – 11x² – 4x + 1 =
– 4x² – 4x + 1

08. a) do retângulo 1. ax
b) do retângulo 2. bx
c) do retângulo 3. ay
d) do retângulo 4. by
e) da figura toda. ax + bx + ay + by

09. a) o volume do sólido 1. x³
b) o volume do sólido 2. x²y
c) o volume do sólido todo. x³ + x²y

10. 2r + ( – s + rs ) – ( r + 3rs – 5s )
2r – s + rs – r – 3rs + 5s =
2r – r – s + 5s – 3rs + rs =
r + 4s – 2rs =
Valor numérico:
r + 4s – 2rs
2 + 4 (-2) – 2. 2.(-2)=
2 – 8 + 8 =
2

11. ab – ( – 2a + b ) – ( c + 3a – ab ) + ( 4a – c )
ab + 2a – b – c – 3a + ab + 4a – c =
ab + ab + 2a + 4a – b – c – c =
2ab + 6a – b – 2c

12. 2xy + 1xy²/2 – 2x²y/3 – xy² + 1xy/4 + 1x²y/6
2xy + 1xy/4 + 1xy²/2 – xy² – 2x²y/3 + 1x²y/6 =
9xy/4 – 1xy²/2 – 1x²y/2

13. 8x³ – ( x² + 7x – 5 ) + ( – 2x³ + 6x² – x ) – ( – 1 + 3x )
8x³ – x² – 7x + 5 – 2x³ + 6x² – x + 1 – 3x² =
8x³ – 2x³ – x² + 6x² – 3x² – 7x – x + 5 + 1 =
6x³ + 2x² – 8x + 6

14. a) da figura 1 . x²
b) da figura 2. ax
c) da figura 3. a²
d) da figura toda. x² + ax + a²

15. x – ( – 5y + 3x ) + ( xy – x – y ) – ( 7y + 2xy )
x + 5y – 3x + xy – x – y – 7y – 2xy =
x – x – 3x + 5y – y – 7y + xy – 2xy =
– 3x – 3y – xy

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína