Questão 01 sobre Polinômios: (UFMG) Sejam p(x) = 4x3 + bx2 + cx + d e q(x) = mx2 + nx – 3, polinômios com coeficientes reais. Sabe-se que p(x) = (2x – 6).q(x) + x – 10.
Considerando-se essas informações, é INCORRETO afirmar que:
A) se 10 é raiz de q(x), então 10 também é raiz de p(x).
B) p(3) = –7
C) d = 18
D) m = 2
Questão 02. (UFMG–2006) Neste plano cartesiano, está representado o gráfico do polinômio p(x) = ax3 + bx2 + cx + d, sendo a, b, c e d números reais.
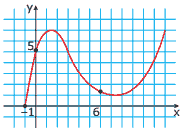
Considere estas afirmativas referentes a esse polinômio:
I. a – b + c – 5 = 0; e
II. p(p(6)) > p(6).
Então, é CORRETO afirmar que:
A) nenhuma das afirmativas é verdadeira.
B) apenas a afirmativa I é verdadeira.
C) apenas a afirmativa II é verdadeira.
D) ambas as afirmativas são verdadeiras.
Questão 03. (UFMG–2007) Sejam p(x) = ax2 + (a – 15)x + 1 e q(x) = 2x2 – 3x + polinômios com coeficientes reais. Sabe-se que esses polinômios possuem as mesmas raízes.
Então, é CORRETO afirmar que o valor de a + b é:
A) 3
B) 6
C) 9
D) 12
Questão 04 sobre Polinômios: (UFOP-MG–2007) O resto da divisão do polinômio p(x)= x99 – 2x + 3 pelo polinômio q(x) = x2 – 1 é:
A) –x + 3
B) 6
C) 8
D) 3x – 1
Questão 05. (PUC Rio) Se x2 + 2x + 5 divide x4 + px2 + q exatamente (isto é, o resto da divisão do segundo polinômio pelo primeiro é zero), então:
A) p = –2 e q = 5
B) p = 5 e q = 25
C) p = 10 e q = 20
D) p = 6 e q = 25
E) p = 14 e q = 25
Questão 06. (UFJF-MG) Ao dividirmos um polinômio p(x) por outro polinômio q(x), encontramos um resto r(x) = x – 1. É CORRETO afirmar que o:
A) grau de p(x) é igual a 2.
B) grau de q(x) é igual a 2.
C) grau de q(x) é maior que 1.
D) grau de p(x) é igual a 1.
Questão 07 sobre Polinômios: (UFES) O polinômio P(x), quando dividido por x2 + x + 1, fornece o quociente x + 1 e o resto x – 1. O coeficiente do termo do primeiro grau no polinômio P(x) é:
A) 0
B) 1
C) 2
D) 3
E) 4
Questão 08. (UFV-MG) O resto da divisão do polinômio p(x) = 5x3 – 4×22 + mx + n pelo polinômio q(x) = x2 – 2x + 1 é r(x) = 3x + 2. Então, o produto mn é igual a:
A) 32
B) –32
C) –16
D) 16
E) 12
Questão 09. (UFRGS) Sabendo-se que o polinômio x4 + 4x3 + px2 + qx + r é divisível por x3 + 3x2 + 9x + 3, segue que p é igual a:
A) 3
B) 6
C) 9
D) 12
E) 15
Questão 10 sobre Polinômios: (Enem) Observe a notícia a seguir:
Robô-bombeiro feito no Brasil ensaia entrada no mercado internacional
Por Guilherme Felitti, repórter do IDG Now! Publicada em 19 de out. de 2006 às 18h19 Atualizada em 20 de out. de 2006 às 11h17
São Paulo – Desenvolvido em Fortaleza para combater incêndios, SACI já é testado pela Petrobrás e desperta interesses nos EUA, Índia e Austrália.

Além de dálmatas, bombeiros poderão ter outra companhia dentro das brigadas a partir de 2007, com funções mais interessantes que os cães malhados.
O robô-bombeiro SACI, construído como projeto de conclusão por um grupo do curso de Engenharia da Computação da Universidade de Fortaleza, deverá começar a ganhar o mundo já no próximo ano.
Já usado em testes dentro da Petrobrás, o robô, que tem a sigla de Sistema de Apoio ao Combate de Incidentes como nome, está em sua terceira versão e será vendido para a Brigada de Chicago até o final do ano.
“O Corpo de Bombeiros da cidade entrou em contato para adquirir uma unidade que subisse escadas”,afirma Roberto Macedo, diretor técnico de pesquisa e desenvolvimento da Armtec, responsável pelo SACI.
Considere que o robô descrito anteriormente se desloque ao longo do gráfico do polinômio P(x) = x3 – 7x2 + 14x – 8. O sistema cartesiano de eixos foi posicionado de modo que as raízes reais desse polinômio indicam possíveis focos de incêndio, os quais serão combatidos pelo robô.
Portanto, pode-se afirmar que o robô bombeiro será utilizado:
A) Nenhuma vez
B) uma vez.
C) duas vezes.
D) três vezes.
E) quatro vezes.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista com 10 Exercícios de Matemática sobre Polinômios:
01. C;
02. D;
03. C;
04. A;
05. D;
06. C;
07. D;
08. B;
09. D;
10. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
