Questão 01 sobre Áreas: (Enem 2011) Em uma certa cidade, os moradores de um bairro carente de espaços de lazer reivindicam à prefeitura municipal a construção de uma praça. A prefeitura concorda com a solicitação e afirma que irá construí-la em formato retangular devido às características técnicas do terreno. Restrições de natureza orçamentária impõem que sejam gastos, no máximo, 180 m de tela para cercar a praça.
A prefeitura apresenta aos moradores desse bairro as medidas dos terrenos disponíveis para a construção da praça:
Terreno 1: 55 m por 45 m
Terreno 2: 55 m por 55 m
Terreno 3: 60 m por 30 m
Terreno 4: 70 m por 20 m
Terreno 5: 95 m por 85 m
Para optar pelo terreno de maior área, que atenda às restrições impostas pela prefeitura, os moradores deverão escolher o terreno
a) 01.
b) 02.
c) 3.
d) 4.
e) 5.
Questão 02. (Enem 2010) A loja Telas & Molduras cobra 20 reais por metro quadrado de tela, 15 reais por metro linear de moldura, mais uma taxa fixa de entrega de 10 reais.
Uma artista plástica precisa encomendar telas e molduras a essa loja, suficientes para 8 quadros retangulares (25 cm x 50 cm). Em seguida, fez uma segunda encomenda, mas agora para 8 quadros retangulares (50 cm x 100 cm). O valor da segunda encomenda será
a) o dobro do valor da primeira encomenda, porque a altura e a largura dos quadros dobraram.
b) maior do que o valor da primeira encomenda, mas não o dobro.
c) a metade do valor da primeira encomenda, porque a altura e a largura dos quadros dobraram.
d) menor do que o valor da primeira encomenda, mas não a metade.
e) igual ao valor da primeira encomenda, porque o custo de entrega será o mesmo.
Questão 03. (Enem 2010) Uma metalúrgica recebeu uma encomenda para fabricar, em grande quantidade, uma peça com o formato de um prisma reto com base triangular, cujas dimensões da base são 6 cm, 8 cm e 10 cm e cuja altura é 10 cm. Tal peça deve ser vazada de tal maneira que a perfuração na forma de um cilindro circular reto seja tangente as suas faces laterais, conforme mostra a figura.
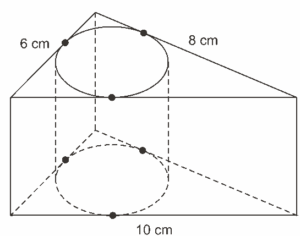
O raio da perfuração da peça é igual a
a) 1 cm.
b) 2 cm.
c) 3 cm.
d) 4 cm.
e) 5 cm.
Questão 04 sobre Áreas: (Enem 2009) O quadro apresenta informações da área aproximada de cada bioma brasileiro.
| biomas continentais brasileiros | área aproximada (Km2) | Área / total Brasil |
| Amazônia | 4.196.943 | 49,29% |
| Cerrado | 2.036.448 | 23,92% |
| Mata atlântica | 1.110.182 | 13,04% |
| Caantiga | 844.453 | 9,92% |
| Pampa | 176.496 | 2,07% |
| Pantanal | 150.355 | 1,76% |
| Área Total Brasil | 8.514.877 |
Disponível em: www.ibge.gov.br. Acesso em: 10 jul. 2009 (adaptado).
É comum em conversas informais, ou mesmo em noticiários, o uso de múltiplos da área de um campo de futebol (com as medidas de 120 m x 90 m) para auxiliar a visualização de áreas consideradas extensas. Nesse caso, qual é o número de campos de futebol correspondente à área aproximada do bioma Pantanal?
a) 1.400
b) 14.000
c) 140.000
d) 1.400.000
e) 14.000.000
Questão 05 sobre Áreas: (Enem 2009) A vazão do rio Tietê, em São Paulo, constitui preocupação constante nos períodos chuvosos. Em alguns trechos, são construídas canaletas para controlar o fluxo de água. Uma dessas canaletas, cujo corte vertical determina a forma de um trapézio isósceles, tem as medidas especificadas na figura I. Neste caso, a vazão da água é de 1.050 m3/s. O cálculo da vazão, Q em m3/s, envolve o produto da área A do setor transversal (por onde passa a água), em m2, pela velocidade da água no local, v, em m/s, ou seja, Q = Av. Planeja-se uma reforma na canaleta, com as dimensões especificadas na figura II, para evitar a ocorrência de enchentes.
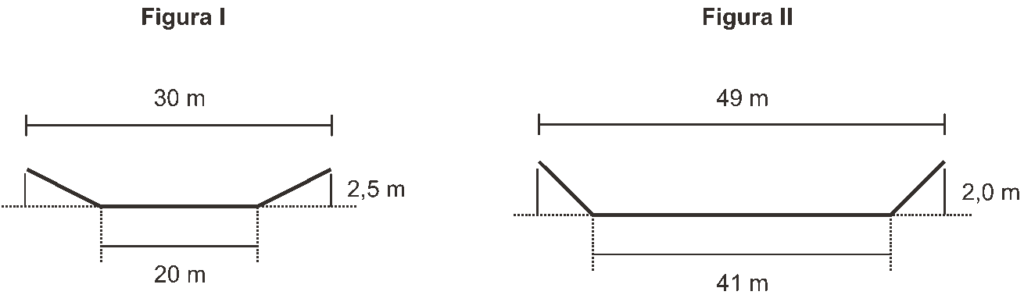
Na suposição de que a velocidade da água não se alterará, qual a vazão esperada para depois da reforma na canaleta?
a) 90 m3/s.
b) 750 m3/s.
c) 1.050 m3/s.
d) 1.512 m3/s.
e) 2.009 m3/s.
Questão 06. (Enem cancelado 2009) Uma fotografia tirada em uma câmera digital é formada por um grande número de pontos, denominados pixels. Comercialmente, a resolução de uma câmera digital é especificada indicando os milhões de pixels, ou seja, os megapixels de que são constituídas as suas fotos.
Ao se imprimir uma foto digital em papel fotográfico, esses pontos devem ser pequenos para que não sejam distinguíveis a olho nu. A resolução de uma impressora é indicada pelo termo dpi (dotper inch), que é a quantidade de pontos que serão impressos em uma linha com uma polegada de comprimento. Uma foto impressa com 300 dpi, que corresponde a cerca de 120 pontos por centímetro, terá boa qualidade visual, já que os pontos serão tão pequenos, que o olho não será capaz de vê-los separados e passará a ver um padrão contínuo.
Para se imprimir uma foto retangular de 15 cm por 20 cm, com resolução de pelo menos 300 dpi, qual é o valor aproximado de megapixels que a foto terá?
a) 1,00 megapixel.
b) 2,52 megapixels.
c) 2,70 megapixels.
d) 3,15 megapixels.
e) 4,32 megapixels.
Questão 07 sobre Áreas: (Enem cancelado 2009) Um fazendeiro doa, como incentivo, uma área retangular de sua fazenda para seu filho, que está indicada na figura como 100% cultivada. De acordo com as leis, deve-se ter uma reserva legal de 20% de sua área total. Assim, o pai resolve doar mais uma parte para compor a reserva para o filho, conforme a figura.
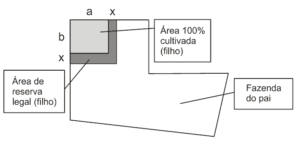
De acordo com a figura anterior, o novo terreno do filho cumpre a lei, após acrescentar uma faixa de largura x metros contornando o terreno cultivado, que se destinará à reserva legal (filho). O dobro da largura x da faixa é
a) 10%(a + b)2
b) 10%(a . b)2
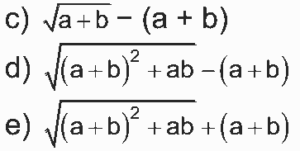
Questão 08 sobre Áreas: (Enem cancelado 2009) Um chefe de cozinha utiliza um instrumento cilíndrico afiado para retirar parte do miolo de uma laranja. Em seguida, ele fatia toda a laranja em secções perpendiculares ao corte feito pelo cilindro. Considere que o raio do cilindro e da laranja sejam iguais a 1 cm e a 3 cm, respectivamente.
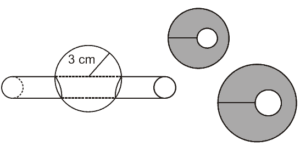
A área da maior fatia possível é
a) duas vezes a área da secção transversal do cilindro.
b) três vezes a área da secção transversal do cilindro.
c) quatro vezes a área da secção transversal do cilindro.
d) seis vezes a área da secção transversal do cilindro.
e) oito vezes a área da secção transversal do cilindro.
Questão 09. (Enem cancelado 2009) Dois holofotes iguais, situados em H1 e H2, respectivamente, iluminam regiões circulares, ambas de raio R. Essas regiões se sobrepõem e determinam uma região S de maior intensidade luminosa, conforme figura.
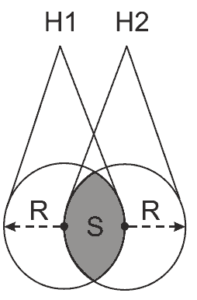
Área do setor circular: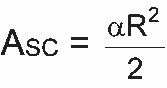 
, α em radianos. A área da região S, em unidades de área, é igual a:
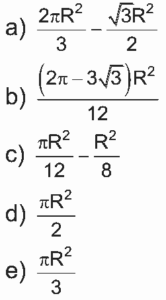
Questão 10 sobre Áreas: (Enem 2009) O governo cedeu terrenos para que famílias construíssem suas residências com a condição de que no mínimo 94% da área do terreno fosse mantida como área de preservação ambiental. Ao receber o terreno retangular ABCD, em que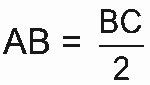 
, Antônio demarcou uma área quadrada no vértice A, para a construção de sua residência, de acordo com o desenho, no qual 
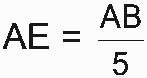é lado do quadrado.
Nesse caso, a área definida por Antônio atingiria exatamente o limite determinado pela condição se ele
a) duplicasse a medida do lado do quadrado.
b) triplicasse a medida do lado do quadrado.
c) triplicasse a área do quadrado.
d) ampliasse a medida do lado do quadrado em 4%.
e) ampliasse a área do quadrado em 4%.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos 10 exercícios de matemática sobre Áreas para passar no Enem e Vestibular:
01. C;
02. B
Valor da primeira encomenda = 8.0,25.0,50.20 + 8.2(0,25 + 0,50).15 + 10 = 20 + 180 + 10 = 210,00.
Valor da segunda encomenda = 8.0,50.1.20 + 8.2(1 + 0,5). 15 + 10 = 80 + 360 + 10 = 450,0.
Logo, o valor da segunda encomenda será maior que o valor da primeira encomenda, mas não o dobro.
03. B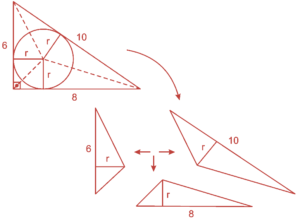
Seja r o raio da base do cilindro O triângulo é retângulo, pois 62 + 82 = 102. Logo, sua área será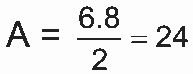 
Portanto: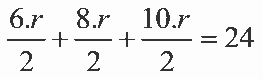 
12r = 24
r = 2
04. E
Área de um campo de futebol (km2) 0,12km . 0,09 km = 0,0108km2 número de campos de futebol para a área do Pantanal = 150.355 dividido por 0,0108 = 13.921759 aproximadamente 14 000 000 km2.
05. D
Área da figura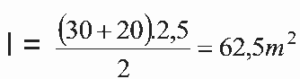 
e seja v a velocidade da água. 1050 = v.62,5 <-> v = 16,8 m/s.
Área da figura II =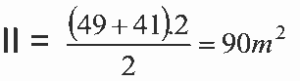 
Nova vazão = 90.16,8 = 1512m3/ s
06. E
12.120 = 1800 pontos
20.120 = 2400 pontos
No retângulo todo 1800.2400 = 4320000 = 4,32.106 pixels ou seja 4,32 megapixels
07. D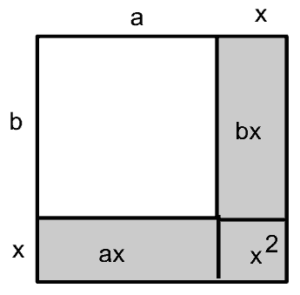
0,2 (a + x) . (b + x) = ax + bx + x2
Desenvolvendo, temos a equação:
0,8x2 + 0,8 (a + b)x – 0,2ab = 0 ( multiplicando por 5)
4x2 + 4 (a+b)x – ab = 0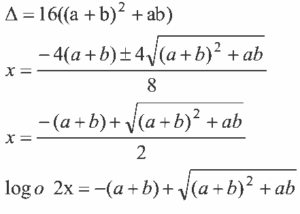
08. E
Área da secção transversal do cilindro: A 1 = π.12 = πcm2
Área da maior fatia: A2 = π.32 – π.12 = 8π cm2
Logo a área da maior fatia será 8 vezes a área da secção transversal do cilindro.
09. A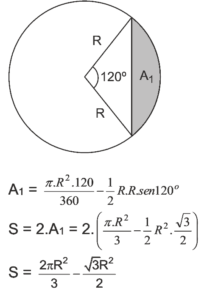
10.C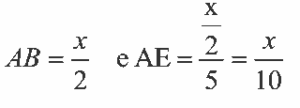
Área da residência =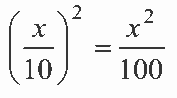 
Área máxima permitida =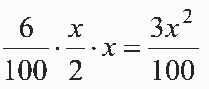 
logo A(máxima) = 3.A(construída)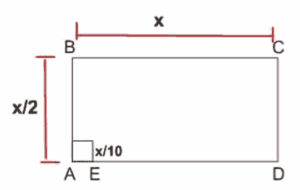
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína