Questão 01. (UFMG) Exercícios sobre Gráficos de Funções: Na figura, estão esboçados os gráficos de duas funções f e g. O conjunto {x ∈ ℝ: f(x).g(x) < 0} é dado por 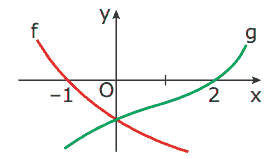
A) x > 0 ou x < –1
B) –1 < x < 0
C) 0 < x < 2
D) –1 < x < 2
E) x < –1 ou x > 2
Questão 02. (UFMG) Dos gráficos, o ÚNICO que representa uma função de imagem {y ∈ ℝ: 1 ≤ y ≤ 4} e domínio {x ∈ ℝ: 0 ≤ x < 3} é:
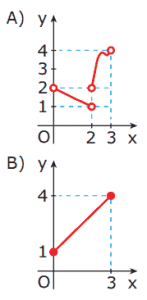
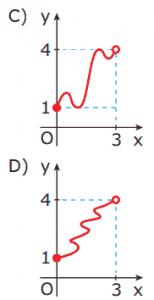
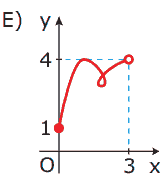
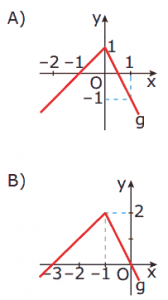
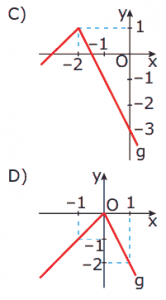
Questão 03. (UFU-MG) Se f é uma função cujo gráfico é dado a seguir, então o gráfico da função g, tal que g(x) = f(x – 1), será dado por: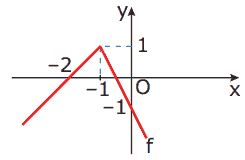
Questão 04. (UFMG) Exercícios sobre Gráficos de Funções: Suponha-se que o número f(x) de funcionários necessários para distribuir, em um dia, contas de luz entre x por cento de moradores, numa determinada cidade, seja dado pela função f(x) = . Se o número de funcionários necessários para distribuir, em um dia, as contas de luz foi 75, a porcentagem de moradores que as receberam é:
A) 25
B) 30
C) 40
D) 45
E) 50
Questão 05. (UFMG) Em uma experiência realizada com camundongos, foi observado que o tempo requerido para um camundongo percorrer um labirinto, na enésima tentativa, era dado pela função f(n) = minutos. Com relação a essa experiência, pode-se afirmar que um camundongo:
A) consegue percorrer o labirinto em menos de três minutos.
B) gasta cinco minutos e 40 segundos para percorrer o labirinto na quinta tentativa.
C) gasta oito minutos para percorrer o labirinto na terceira tentativa.
D) percorre o labirinto em quatro minutos na décima tentativa.
E) percorre o labirinto, numa das tentativas, em três minutos e 30 segundos.
Questão 06. (Enem–2002) O excesso de peso pode prejudicar o desempenho de um atleta profissional em corridas de longa distância como a maratona (42,2 km), a meia-maratona (21,1 km) ou uma prova de 10 km. Para saber uma aproximação do intervalo de tempo a mais perdido para completar uma corrida devido ao excesso de peso, muitos atletas utilizam os dados apresentados na tabela e no gráfico.
| Altura (m) | peso (Kg) ideal para atleta masculino de ossatura grande, corredor de longa distância |
| 1,57 | 56,9 |
| 1,58 | 57,4 |
| 1,59 | 58,0 |
| 1,60 | 58,5 |
| … | … |
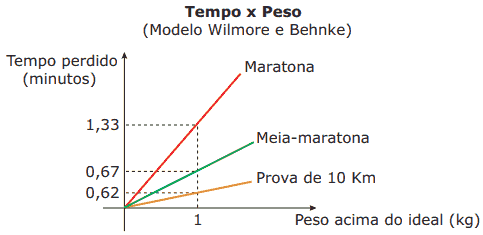
Usando essas informações, um atleta de ossatura grande, pesando 63 kg e com altura igual a 1,59 m, que tenha corrido uma meia-maratona, pode estimar que, em condições de peso ideal, teria melhorado seu tempo na prova em:
A) 0,32 minuto.
B) 0,67 minuto.
C) 1,60 minuto.
D) 2,68 minutos.
E) 3,35 minutos.
Questão 07. (UECE) Exercícios sobre Gráficos de Funções: Seja f: ℝ → ℝ a função tal que f(1) = 4 e f(x + 1) = 4 f(x) para todo real. Nessas condições, f(10) é igual a:
A) 2-10
B) 4-10
C) 210
D) 410
Questão 08. (UFMG–2008) Neste plano cartesiano, estão representados os gráficos das funções y = f(x) e y = g(x), ambas definidas no intervalo aberto ]0, 6[.
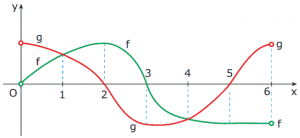
Seja s o subconjunto de números reais definido por S = {x ∈ ℝ; f(x).g(x) < 0}. Então, é CORRETO afirmar que s é:
A) {x ∈ ℝ; 2 < x < 3} ∪ {x ∈ ℝ; 5 < x < 6}
B) {x ∈ ℝ; 1 < x < 2} ∪ {x ∈ ℝ; 4 < x < 5}
C) {x ∈ ℝ; 0 < x < 2} ∪ {x ∈ ℝ; 3 < x < 5}
D) {x ∈ ℝ; 0 < x < 1} ∪ {x ∈ ℝ; 3 < x < 6}
Questão 09. (CEFET-MG–2009) Sejam a função real f, do segundo grau, definida graficamente por
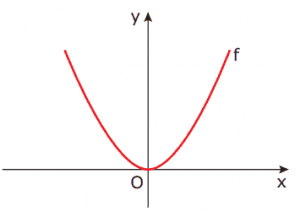
e k uma constante real tal que k > 0. O gráfico que MELHOR representa a função g tal que g(x) = f(x – k) + k é
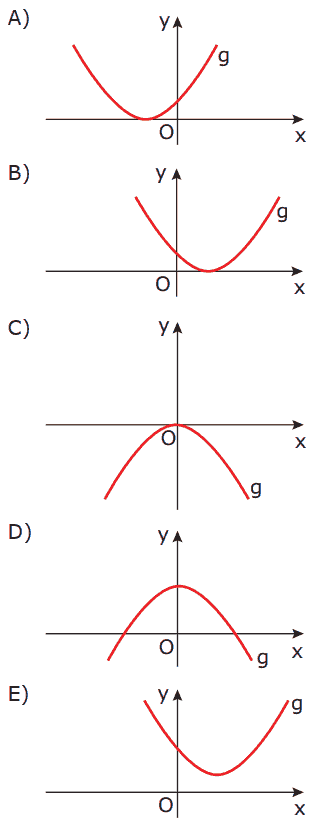
Questão 10. (Mackenzie-SP) Exercícios sobre Gráficos de Funções: Se a curva dada é o gráfico da função y = a + , então o valor de ab é:
A)
B) √3
C) 2
D) 4
E)

Gabarito com as respostas da lista de exercícios sobre Gráficos de Funções para alunos e professores:
01. E;
02. C;
03. A;
04. B;
05. E;
06. E;
07. D;
08. A;
09. E;
10. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
