Questão 01 sobre Plano Cartesiano: (UFU-MG) Considere, no plano cartesiano com origem o, um triângulo cujos vértices A, B e C têm coordenadas (–1, 0), (0, 4) e (2, 0), respectivamente. Se M e N são os pontos médios de AB e BC, respectivamente, a área do triângulo OMN será igual a
A) 
u.a.
B) u.a.
C) 1 u.a.
D) u.a.
Questão 02. ENEM. Considere um ponto P em uma circunferência de raio r no plano cartesiano. Seja Q a projeção ortogonal de P sobre o eixo x, como mostra a figura, e suponha que o ponto P percorra, no sentido anti-horário, uma distância d ≤ r sobre a circunferência.
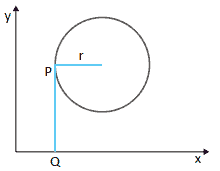
Então, o ponto Q percorrerá, no eixo x, uma distância dada por:
A) r 
B) r 
C) r 
D) rsen 
E) rcos
Questão 03. (UFMG–2006) Neste plano cartesiano, está representado o quadrilátero AbCD.
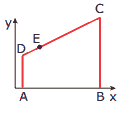
sabe-se que:
I) A(1, 0), C(11, 11) e E(3, 7).
II) o ponto B está no eixo x e o ponto E, no lado 
.
III) os lados 
e são paralelos ao eixo y.
Então, é Correto afirmar que a área do quadrilátero ABCD é
A) 87,5
B) 82,5
C) 85
D) 86
Questão 04. (FUVEST-SP) Na figura a seguir, a é um ponto do plano cartesiano, com coordenadas (x, y). sabendo que a está localizado abaixo da reta r e acima da reta s, tem-se:
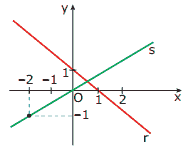
A) y < 
e y < –x + 1
b) y < ou y > –x + 1
C) < y e y > –x + 1
D) –x + 1 < y <
E) < y < –x + 1
Questão 05. (UFJF) A figura abaixo é um esboço do gráfico da função y = 2x no plano cartesiano.
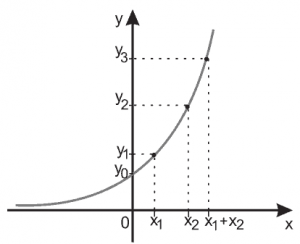
Com base nesse gráfico, é correto afirmar que:
A) y0 = y2 − y1
B) y1 = y3 − y2
C) y1 = y3 + y0
D) y2 = y1 ⋅ y0
E) y3 = y1 ⋅ y2
Questão 06. (PUC-sP) O conjunto dos pontos (x, y) do plano cartesiano que satisfazem a inequação (x + y)(x – y) ≤ 0 é a parte hachurada de qual das seguintes figuras?
Questão 07. (PUC Minas) Considere a região do plano cartesiano formada pelos pontos cujas coordenadas satisfazem ao
Sistema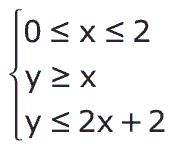 
Tomando-se o metro como unidade de medida nos eixos coordenados, essa região é um trapézio com 2 m de altura e área igual a a metros quadrados.
Então, o valor de a é:
A) 3
B) 4
C) 5
D) 6
Questão 08. (UFC–2008) O número de pontos na interseção dos subconjuntos do plano cartesiano:
r = {(x, y) ∈ 
2; –x + y + 1 = 0} e
c = {(x, y) ∈ 2; x2 + y2 + 2x – 4y + 1 = 0} é
A) 0
b) 1
C) 2
D) 3
E) 4
Questão 09. (FUVEST-SP) Das regiões hachuradas na sequência, a que MELHOR representa o conjunto dos pontos (x, y), do plano cartesiano, satisfazendo ao conjunto de desigualdades x ≥ 0; y ≥ 0; x – y + 1 ≥ 0; x2 + y2 ≤ 9, é
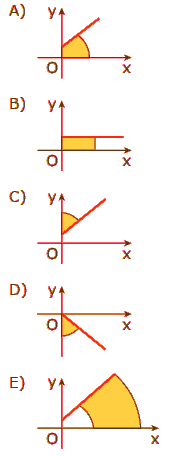
Questão 10 sobre Plano Cartesiano: (Enem) Um emblema de uma bandeira de uma escola de samba é uma figura geométrica definida por x2 + y2 – 6x – 6y + 9 ≤ 0 quando projetada em um plano cartesiano com x e y dados em metros. Esse emblema será pintado em duas cores separadas pela reta y = x. A região acima da reta será pintada de verde, e a região abaixo será pintada de rosa. Considerando que a escola de samba pretende confeccionar 100 dessas bandeiras e que uma lata de tinta cobre 4 m2 do emblema, determine a quantidade mínima de latas de tinta rosa a serem utilizadas. Adote p = 3,14.
A) 225
b) 320
C) 354
D) 450
E) 500
>>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas do simulado com 10 exercícios de matemática sobre Plano Cartesiano:
01. D;
02. B;
03. C;
04. E;
05. E;
06. E;
07. D;
08. A;
09. A;
10. C
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína