Questão 01 sobre Hidrostática Densidade e pressão: (Utfpr) Em uma proveta que contém 100 cm3 de água, é colocada cuidadosamente uma pepita de ouro com massa de 152 g. Observa-se que o nível da água aumenta para 108 cm3. Qual a densidade da pepita?
a) 15,2 g/cm3.
b) 14 g/cm3.
c) 19 g/cm3.
d) 15,2 kg/m3.
e) 14 kg/m3.
Questão 02. Modelo Enem. Uma criança boiando na água de uma piscina, ao inspirar o ar e mantê-lo, por alguns segundos, preso nos pulmões, percebe sua elevação em relação ao nível da água. Esse fato pode ser descrito pela(o)
a) aumento do peso da água deslocada.
b) aumento do empuxo da água da piscina.
c) diminuição da densidade média da criança.
d) diminuição da densidade da água da piscina.
Questão 03. (Fuvest) A janela retangular de um avião, cuja cabine é pressurizada, mede 0,5 m por 0,25 m. Quando o avião está voando a uma certa altitude, a pressão em seu interior é de, aproximadamente, 1,0 atm, enquanto a pressão ambiente fora do avião é de 0,60 atm. Nessas condições, a janela está sujeita a uma força, dirigida de dentro para fora, igual ao peso, na superfície da Terra, da massa de
a) 50 kg
b) 320 kg
c) 480 kg
d) 500 kg
e) 750 kg
obs.: 1 atm = 105 Pa = 105 N/m2
Questão 04 sobre Hidrostática Densidade e pressão: (Unesp) Em uma competição esportiva, um halterofilista de 80 kg, levantando uma barra metálica de 120 kg, apoia-se sobre os seus pés, cuja área de contato com o piso é de 25 cm2. Considerando g = 10 m/s2 e lembrando-se de que a pressão é o efeito produzido por uma força sobre uma área e considerando que essa força atua uniformemente sobre toda a extensão da área de contato, a pressão exercida pelo halterofilista sobre o piso, em pascal, é de:
a) 2 × 105.
b) 8 × 105.
c) 12 × 105.
d) 25 × 105.
e) 2 × 106.
Questão 05. (Unesp) O tubo aberto em forma de U da figura contém dois líquidos não miscíveis, A e B, em equilíbrio. As alturas das colunas de A e B, medidas em relação à linha de separação dos dois líquidos, valem 50 cm e 80 cm, respectivamente.
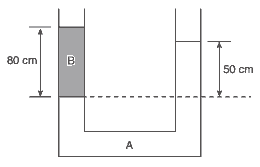
a) Sabendo que a massa específica de A é 2,0 × 103 kg/m3, determine a massa específica do líquido B.
b) Considerando g = 10 m/s2 e a pressão atmosférica igual a 1,0 × 105 N/m2, determine a pressão no interior do tubo na altura da linha de separação dos dois líquidos.
Questão 06. (Ufpr) Com o objetivo de encontrar grande quantidade de seres vivos nas profundezas do mar, pesquisadores utilizando um submarino chegaram até a profundidade de 3.600 m no Platô de São Paulo. A pressão interna no submarino foi mantida igual à pressão atmosférica ao nível do mar. Considere que a pressão atmosférica ao nível do mar é de 1,0 × 105 N/m2 a aceleração da gravidade é 10 m/s2 e que a densidade da água seja constante e igual a 1,0 × 103 kg/m3. Com base nos conceitos de hidrostática, assinale a alternativa que indica quantas vezes a pressão externa da água sobre o submarino, naquela profundidade, é maior que a pressão no seu interior, se o submarino repousa no fundo do platô.
a) 10.
b) 36.
c) 361.
d) 3610.
e) 72000.
Questão 07 sobre Hidrostática Densidade e pressão: (Pucrs) Aquecedores de passagem são acionados pela passagem da água no seu interior, ou seja, ligam quando a torneira é aberta. O manual de instalação de um aquecedor deste tipo informa que “a pressão mínima necessária para o correto funcionamento do equipamento é equivalente a 10 m de coluna de água”.
Levando-se em conta que a massa específica da água é 1000 kg/m3 e a aceleração da gravidade no local é aproximadamente 10 m/s2, a informação se refere à pressão hidrostática, em pascais, de
a) 1,0 × 106
b) 1,0 × 105
c) 1,0 × 104
d) 1,0 × 103
e) 1,0 × 102
Questão 08. (Unicamp) Durante uma tempestade de 20 minutos, 10 mm de chuva caíram sobre uma região cuja área total é 100 km2.
a) Sendo que a densidade da água é de 1,0 g/cm3, qual a massa de água que caiu?
b) A partir de uma estimativa do volume de uma gota de chuva, calcule o número médio de gotas que caem em 1 m2 durante 1 s.
Questão 09. (Unicamp) Se dois corpos têm todas as suas dimensões lineares proporcionais por um fator de escala b, então a razão entre suas superfícies é b2 e entre seus volumes é b3. Seres vivos perdem água por evaporação proporcionalmente às suas superfícies. Então eles devem ingerir líquidos regularmente para repor essas perdas de água. Considere um homem e uma criança com todas as dimensões proporcionais. Considere ainda que o homem têm 80 kg; 1,80 m de altura e bebe 1,2 litros de água por dia para repor as perdas devidas apenas à evaporação.
a) Se a altura da criança é 0,90 m, qual é o seu peso?
b) Quantos litros de água por dia ela deve beber apenas para repor suas perdas por evaporação?
Questão 10 sobre Hidrostática Densidade e pressão: (Unicamp) “Os grandes problemas contemporâneos de saúde pública exigem a atuação eficiente do Estado que, visando à proteção da saúde da população, emprega tanto os mecanismos de persuasão (informação, fomento), quanto os meios materiais (execução de serviços) e as tradicionais medidas de polícia administrativa (condicionamento e limitação da liberdade individual). Exemplar na implementação de política pública é o caso da dengue, que se expandiu e tem-se apresentado em algumas cidades brasileiras na forma epidêmica clássica, com perspectiva de ocorrências hemorrágicas de elevada letalidade. Um importante desafio no combate à dengue tem sido o acesso aos ambientes particulares, pois os profissionais dos serviços de controle encontram, muitas vezes, os imóveis fechados ou são impedidos pelos proprietários de penetrarem nos recintos. Dada a grande capacidade dispersiva do mosquito vetor, ‘Aedes aegypti’, todo o esforço de controle pode ser comprometido caso os operadores de campo não tenham acesso às habitações.
(Adaptado de “Programa Nacional de Controle da Dengue”. Brasília: Fundação Nacional de Saúde, 2002.)
O texto se refere ao combate ao mosquito vetor da dengue. Um parâmetro importante usado no acompanhamento da proliferação da dengue nas grandes cidades é o raio de voo do mosquito, que consiste na distância máxima dentro da qual ele pode ser encontrado a partir do seu local de origem. Esse raio, que em geral varia de algumas centenas de metros a poucos quilômetros, é na verdade muito menor que a capacidade de deslocamento do mosquito.
a) Considere que o mosquito permanece em voo cerca de 2 horas por dia, com uma velocidade média de 0,50 m/s. Sendo o seu tempo de vida igual a 30 dias, calcule a distância percorrida (comprimento total da trajetória) pelo mosquito durante a sua vida.
b) Assumindo que a pressão necessária para perfurar a pele humana seja P = 2,0 ⋅ 107 N/m2, calcule a força mínima que deve ser exercida pelo mosquito na sua picada. A área do seu aparelho bucal picador em contato com a pele é A = 2,5 ⋅ 10-11 m2.
🔵 >>> Verifique todos os nossos exercícios e atividades de Física.
Gabarito com as respostas da lista com 10 exercícios de física sobre Hidrostática Densidade e Pressão:
01. C;
02. c;
03. d;
04. b;
05. a. 1,2.103kg/m3
b. 1,1.105Pa
06. c;
07. b;
08. a. 1,0 × 109 kg
b. 167 gotas
09. a. 98 N.
b. 0,30 ℓ.
10. a. d = 108 km
b. Fmin = 5 . 104 N
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
