Questão 01 sobre Equações Polinominais ou Algébricas: (UFRGS) Sabendo-se que 3 é uma raiz do polinômio P(x) = x3 – 8x2 + 19x – 12, pode-se afirmar que as outras duas raízes são:
a) -1 e 3.
b) 1 e 4.
c) 2 e 4.
d) 1 e 2.
e) -1 e -4.
Questão 02. (Fuvest) O polinômio P(x), dado por x3 – x2 + x – 1, é divisível por x – 1. Ache todas as raízes complexas da equação P(x) = 0.
Questão 03. (PUC-SP) A multiplicidade da raiz 1 da equação x4 – x3 – 3x2 + 5x – 2 = 0 é:
a) 2.
b) 3.
c) 4.
d) 5.
e) 6.
Questão 04 sobre Equações Polinominais ou Algébricas: (Fuvest) O número 2 é raiz dupla de ax3 + bx + 16 = 0. Determine a e b.
Questão 05. (Fuvest) O gráfico
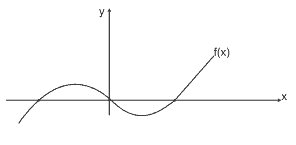
pode representar a função:
a) x(x – 1).
b) x2(x2 – 1).
c) x3(x – 1).
d) x(x2 – 1).
e) x2(x – 1).
Questão 06. (UFMG) Seja f uma função polinomial de terceiro grau, cujo gráfico se encontra parcialmente representado na figura:
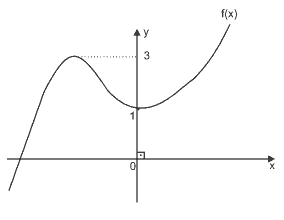
Quantas são as soluções da equação f(x) = 2?
a) 1.
b) 2.
c) 3.
d) 4.
Questão 07 sobre Equações Polinominais ou Algébricas: (FGV-SP) Sobre as raízes da equação 2x3 – x2 – 2x + 1 = 0, é verdade que:
a) nenhuma delas é real.
b) exatamente duas delas são negativas.
c) somente uma delas é irracional.
d) as três são números inteiros.
e) pertencem ao intervalo [-1, 1].
Questão 08. (Fuvest) Uma das raízes da equação x3 + (m + 1)x2 + (m + 9)x + 9 = 0 é -1. Determine os valores reais de m, para que as outras raízes sejam reais.
Questão 09.(Fatec-SP) Se a equação x2 – 10x + k = 0 tem uma raiz de multiplicidade 2, então, o valor de k é:
a) 100.
b) 25.
c) 5.
d) 1.
e) 0.
Questão 10 sobre Equações Polinominais ou Algébricas: (Fuvest) A equação x3 – 8px2 + x – q = 0 admite a raiz 1 com multiplicidade 2. Então, p vale
a) 1/2.
b) 1/3.
c) 1/4.
d) 1/5.
e) 1/6.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos 10 exercícios de matemática sobre Equações Polinominais ou Algébricas:
01) b;
02) S = { 1, i, -i };
03) b;
04) a = 1, b = –12
05) d;
06) c;
07) e;
08) m ≤ -6 ou m ≥ 6;
09) b;
10) c
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
