Questão 01 sobre Conjuntos: Segundo o matemático Leopold Kronecker (1823-1891), “Deus fez os números inteiros, o resto é trabalho do homem.” Os conjuntos numéricos são, como afirma o matemático, uma das grandes invenções humanas.
Assim, em relação aos elementos desses conjuntos, é correto afirmar que:
a) o produto de dois números irracionais é sempre um número irracional.
b) a soma de dois números irracionais é sempre um número irracional.
c) entre os números reais 3 e 4 existe apenas um número irracional.
d) entre dois números racionais distintos existe pelo menos um número racional.
e) a diferença entre dois números inteiros negativos é sempre um número inteiro negativo.
Questão 02. Num colégio de 100 alunos, 80 gostam de sorvete de chocolate, 70 gostam de sorvete de creme e 60 gostam dos dois sabores. Quantos não gostam de nenhum dos dois sabores?
a) 0
b) 10
c) 20
d) 30
e) 40
Questão 03. Um trem viajava com 242 passageiros, dos quais:
– 96 eram brasileiros,
– 64 eram homens,
– 47 eram fumantes,
– 51 eram homens brasileiros,
– 25 eram homens fumantes,
– 36 eram brasileiros fumantes,
– 20 eram homens brasileiros fumantes.
Calcule:
a) o número de mulheres brasileiras não fumantes;
b) o número de homens fumantes não brasileiros;
c) o número de mulheres não brasileiras, não fumantes.
Questão 04 sobre Conjuntos: Numa pesquisa de mercado, verificou-se que 150 pessoas utilizam pelo menos um dos produtos B ou C. Sabendo que 95 dessas pessoas não usam o produto C e 25 não usam o produto B, qual é o número de pessoas que utilizam os produtos B e C?
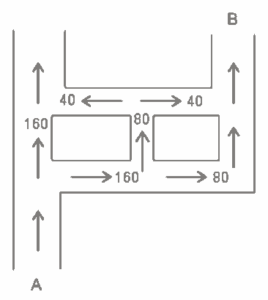
Questão 05. A figura a seguir representa uma região de ruas de mão única. O número de carros se divide igualmente em cada local onde existam duas opções de direções, conforme a figura:
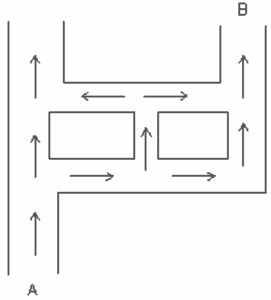
Se 320 carros entram em A, quantos deixam a saída B?
Questão 06.Uma prova com duas questões foi dada a uma classe de quarenta alunos. Dez alunos acertaram as duas questões, 25 acertaram a primeira e 20 acertaram a segunda questão. Quantos alunos erraram as duas questões?
( ) 40
( ) 10
( ) Nenhum
( ) 8
( ) 5
Questão 07. Conjuntos: Em uma turma de 60 alunos, 21 praticam natação e futebol, 39 praticam natação e 33 praticam futebol.
a) Qual a porcentagem de alunos que praticam um, e somente um, desses esportes?
b) Qual a porcentagem de alunos que não praticam nenhum desses esportes?
Questão 08 sobre Conjuntos: “Ah, prometo àqueles meus professores desiludidos que na próxima vida eu vou ser um grande matemático. Porque a Matemática é o único pensamento sem dor.”
Mário Quintana (1906-1994)
Uma sentença matemática verdadeira exemplifica o que o poeta diz ser um “pensamento sem dor”.
Assinale, dentre as alternativas a seguir, aquela que é uma sentença matemática verdadeira:
a) Se x e y ∈ IR e x ≠ 0 e y ≠ 0, então x2 – y2 ≠ 0
b) Se x e y ∈ IR e x2 > y2, então x > y
c) Se x e y ∈ IR e x + 2y ≠ 0, então x2 + y2 ≠ 0
d) Se x e y ∈ IR – {0} e x > y, então 1/x < 1/y
Questão 09. A partir do século XII os cientistas árabes começaram a divulgar seu saber na forma de versos que facilitavam a memorização e divertiam a sociedade. Originalmente, durante os saraus, eram declamados poemas de sátira, de enaltecimento ou recitavam-se versos que deveriam começar pela última letra do verso precedente. Depois, essas atividades foram enriquecidas com enigmas versificados, problemas recreativos e, às vezes, até bilhetes amorosos em forma matemática.
Sabe-se ainda pela mesma fonte, que o matemático árabe Ibn Al-Banna (1256 – 1321) escreveu o seguinte bilhete amoroso em forma de enigma versificado, imaginando seu coração dividido em certo número de partes iguais.
Três sétimos [do número total de partes] do meu coração para seu olhar,
Um sétimo [do número total de partes do meu coração] é oferecido para a rosa de suas
bochechas.
Um sétimo e a metade de um sétimo e o quarto do sétimo [do número total de partes do meu
coração],
Pela recusa de um desejo insatisfeito.
Um sétimo e um sexto de um quarto do sétimo [do número total de partes do meu coração] são a
parte dos seios bem redondos,
Que se recusaram ao pecado do meu abraço e me empurraram.
Sobraram cinco partes, que são pelas palavras dela,
Que estancariam minha sede se tivessem sido escutadas.
(Adaptado do Scientific American Brasil, 11/2005)
Considerando que x é o número total de partes iguais em que o coração do poeta foi dividido, pode-se afirmar que x pertence ao conjunto
a) { x ∈ IN │ 170 < x ≤ 175}
b) { x ∈ IN │ 160 < x ≤ 165}
c) { x ∈ IN │ 155 < x ≤ 160}
d) { x ∈ IN │ 165 < x ≤ 170}
e) { x ∈ IN │ 175 < x ≤ 180}
Questão 10 sobre Conjuntos: Modelo Enem. Numa cidade de 100.000 habitantes, 30.000 são flamenguistas, 12.000 são flamenguistas e corintianos ao mesmo tempo, e o número de habitantes que não são nem flamenguistas nem corintianos é de 39.000. Então o número de corintianos é:
a) 45.000.
b) 35.000.
c) 55.000.
d) 85.000.
e) 43.000.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista com 10 exercícios de matemática sobre Conjuntos:
1. D
a) Falsa, √2.√2 = 2(racional)
b) Falsa, –√2+√2 = 0(racional)
c) Falsa, são infinitos
d) Verdadeira
e) Falsa, -3 –(-5) = 2
2. B;
3. a) 29
b) 5
c) 127
4. 30;
5. De acordo com a figura, segue que o número de carros que deixam a saída B é 80 + 40 = 120.
6. E;
7. a) 50%.
b) 15%.
8. C;
9. D;
10.E
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
