Questão 01 sobre Equações de Circunferência: (UERN 2015) O raio da circunferência determinada pela equação x2 + y2 + 4x – 6y – 3 = 0 é, em unidades de medida:
a) 1.
b) 2.
c) 3.
d) 4.
Questão 02. (UECE 2016) No plano cartesiano usual, a equação da circunferência que contém os pontos (– 4, 0), (4, 0) e (0, 8) é x2 + y2 + my + n = 0. O valor da soma m2 + n é:
a) 30.
b) 10.
c) 40.
d) 20.
Questão 03. (Unicamp 2016) Considere o círculo de equação cartesiana x2 + y2 = ax + by, onde a e b são números reais não nulos. O número de pontos em que esse círculo intercepta os eixos coordenados é igual a:
a) 1.
b) 2.
c) 3.
d) 4.
Questão 04 sobre Equações de Circunferência: (PUC-SP 2016) Na figura tem-se a representação de, circunferência de centro l, e tangente aos eixos coordenados nos pontos A e B.
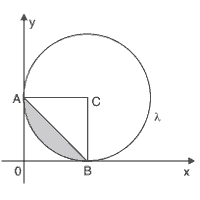
Se a equação de é x2 + y2 – 8x – 8y + 16 = 0, então a área da região hachurada, em unidades de superfície, é:
a) 8 ⋅ (π – 2)
b) 8 ⋅ (π – 4)
c) 4 ⋅ (π – 2)
d) 4 ⋅ (π – 4)
Questão 05. (Uema 2015) Um fabricante de brinquedos utiliza material reciclado: garrafas, latinhas e outros. Um dos brinquedos despertou a atenção de um estudante de Geometria, por ser confeccionado da seguinte forma: amarra-se um barbante em um bico de garrafa pet cortada e, na extremidade, cola-se uma bola de plástico que, ao girar em torno do bico, forma uma circunferência. O estudante representou-a no sistema por coordenadas cartesianas, conforme a figura a seguir:
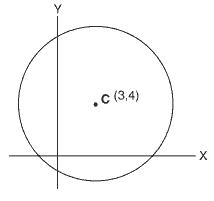
Considerando o tamanho do barbante igual a 6 unidades de comprimento (u.c.) e o bico centrado no ponto (3, 4), a equação que representa a circunferência é igual a:
a) x2 + y2 – 6x – 8y – 11 = 0
b) x2 + y2 + 6x + 8y – 11 = 0
c) x2 + y2 – 6x + 8y + 11 = 0
d) x2 + y2 – 6x – 8y + 11 = 0
e) x2 + y2 – 6x – 8y – 11 = 0
Questão 06. (UFSM 2015) Uma antena de telefone celular rural cobre uma região circular de área igual a 900πkm2. Essa antena está localizada no centro da região circular e sua posição no sistema cartesiano, com medidas em quilômetros, é o ponto (0, 10). Assim, a equação da circunferência que delimita a região circular é:
a) x2 + y2 – 20y – 800 = 0.
b) x2 + y2 – 20y + 70 = 0.
c) x2 + y2 – 20x – 800 = 0.
d) x2 + y2 – 20y – 70 = 0.
e) x2 + y2 = 900.
Questão 07 sobre Equações de Circunferência: Unisc 2015) Observando o círculo abaixo, representado no sistema de coordenadas cartesianas, identifique, entre as alternativas apresentadas, a equação que o representa.
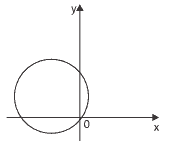
a) x2 + (y + 2)2 = 10.
b) (x + 3)2 + y2 = 10.
c) (x + 3)2 + (y + 2)2 = 13.
d) (x + 3)2 + (y –2)2 = 13.
e) (x –3)2 + (y + 2)2 = 13.
Questão 08. (UEG 2015) Um espelho no formato de circunferência foi pendurado em uma parede. Considerando o canto inferior esquerdo como a origem de um sistema cartesiano, o espelho pode ser representado pela equação da circunferência x2 + y2 – 4x – 7,84 = 0. Dessa forma, constata-se que o espelho está a uma altura do chão de:
a) 1,00 metros.
b) 1,55 metros.
c) 1,60 metros.
d) 1,74 metros.
Questão 09. (Fuvest) O ponto P(2, – 5) é um vértice de um quadrado que tem um dos lados não adjacente a P sobre a reta x – 2y – 7 = 0. Qual a área do quadrado?
Questão 10 sobre Equações de Circunferência: (Fuvest) O centro da circunferência que passa pelos pontos (4, 6) e (– 6, 4) e pertence à reta 3x + y – 12 = 0 é:
a) (6, –2)
b) (– 6, 30)
c) (0, 1)
d) (6, 12)
e) (– 6, 1)
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas das 10 atividades para vestibular sobre Equações de Circunferência:
01) d;
02) d;
03) c;
04) c;
05) a;
06) a;
07) d;
08) c;
09) 5;
10) b
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
