Questão 01. (UFJF-MG) Função Logarítmica Exercícios: A figura a seguir é um esboço, no plano cartesiano, do gráfico da função f(x) = logb x, com alguns pontos destacados. Supondo que a abscissa do ponto A é igual a 9, é INCORRETO afirmar que: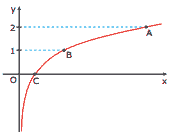
A) a base b é igual a 3.
B) a abscissa de C é igual a 1.
C) f(x) < 0 para todo x ∈ (0, 1).
D) a abscissa de B é igual a 2.
E) f(x) é crescente.
Questão 02. (UNIFESP) Com base na figura, o comprimento da diagonal AC do quadrilátero ABCD, de lados paralelos aos eixos coordenados, é: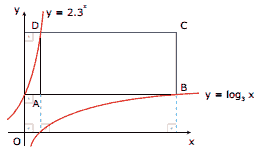
A) 2√2
B) 4√2
C) 8
D) 4√5
E) 6√3
Questão 03. (FGV-SP) A solução da inequação log (x2 – 3) > 0 é:
A) {x ∈ | x < –√3 ou x > √3}
B) {x ∈ | –2 < x < 2}
C) {x ∈ | –√3 < x < √3}
D) {x ∈ | –2 < x < –√3 ou √3 < x < 2}
E) {x ∈ | x < – 2 ou x > 2}
Questão 04. (UFU-MG–2008) Função Logarítmica Exercícios: Se n ∈ e S é o conjunto solução da inequação (log n)2 – 3.(log n) + 2 ≤ 0, então é CORRETO afirmar que:
A) S contém 4 múltiplos de 20.
B) S contém 90 elementos.
C) S contém 46 números ímpares.
D) S contém 46 números pares.
Questão 05. (UNIRIO-RJ) Uma indústria do Rio de Janeiro libera poluentes na Baía de Guanabara. Foi feito um estudo para controlar essa poluição ambiental, cujos resultados são a seguir relatados.

Do ponto de vista da comissão que efetuou o estudo, essa indústria deveria reduzir sua liberação de rejeitos até o nível em que se encontra P, admitindo-se que o custo total ideal é o resultado da adição do custo de poluição y = 2x – 1 ao custo de controle da poluição y = 6 . Para que se consiga o custo ideal, a quantidade de poluentes emitidos, em kg, deve ser, aproximadamente,
Considere: log 2 = 0,3 e log 3 = 0,4:
A) 1 333
B) 2 333
C) 3 333
D) 4 333
E) 5 333
Questão 06. (UFF-RJ) A figura representa o gráfico da função f definida por f(x) = log2 x.
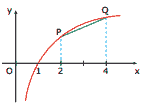
A medida do segmento PQ é igual a:
A) √6
B) √5
C) log2 5
D) 2
E) log 2
Questão 07. (UFOP-MG–2010) Função Logarítmica Exercícios: A população de certo tipo de bactérias estudado por um pesquisador foi modelada da seguinte forma: f(t) = a.log2 (t + 1) + bt2 + 300, onde t representa o tempo em horas no qual o pesquisador começou a observar essa população. O instante t = 0 é o início das observações, quando havia 300 bactérias nessa população. Suponha que, nos instantes t = 1 e t = 3, o número de bactérias era 350 e 540, respectivamente.
Baseando-nos nessas informações, podemos afirmar que o aumento percentual no número de bactérias do instante t = 3 para t = 7 está entre:
A) 65% e 75%.
B) 150% e 160%.
C) 35% e 45%.
D) 180% e 190%.
Questão 08. (UEL-PR–2008) O iodo-131 é um elemento radioativo utilizado em Medicina Nuclear para exames de tireoide e possui meia-vida de 8 dias. Para descarte de material contaminado com 1 g de iodo-131, sem prejuízo para o meio ambiente, o laboratório aguarda que o mesmo fique reduzido a 10-6 g de material radioativo. Nessas condições, o prazo MÍNIMO para descarte do material é de:
Dado: log10 2 ≅ 0,3
A) 20 dias.
B) 90 dias.
C) 140 dias.
D) 160 dias.
E) 200 dias.
Questão 09. Segundo a escala Richter, a magnitude M de um terremoto é dada por:
M = 3,30 + log10 (A.f)
sendo A a amplitude da onda sísmica em micrômetros (mm) e f a frequência da onda, em hertz (Hz). Os efeitos de um terremoto, de acordo com a sua magnitude, são apresentados a seguir:
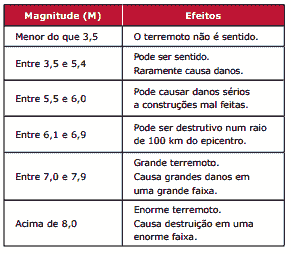
Suponha que um terremoto tenha amplitude de 2 000 mm e frequência de 0,1 Hz. Acerca desse terremoto, é possível afirmar que:
(Considere: log10 2 = 0,30)
A) o terremoto não é sentido.
B) sua magnitude encontra-se entre 5,5 e 6,0.
C) é um grande terremoto.
D) sua magnitude é igual a 6,2.
E) é duas vezes mais destrutivo do que um terremoto com frequência 0,05 Hz.
Questão 10. (UFMG–2006) Função Logarítmica Exercícios: Neste plano cartesiano, estão representados o gráfico da função y = log2 x e o retângulo ABCD, cujos lados são paralelos aos eixos coordenados.
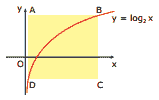
Sabe-se que:
I) os pontos B e D pertencem ao gráfico da função y = log2 x.
II) as abscissas dos pontos A e B são, respectivamente, 1 4 e 8.
Então, é CORRETO afirmar que a área do retângulo ABCD é:
A) 38,75
B) 38
C) 38,25
D) 38,5
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas do simulado de Matemática sobre Função Logarítmica Exercícios:
01. E;
02. D;
03. D;
04. D;
05. A;
06. B;
07. B;
08. D;
09. B;
10. A
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
