Questão 01 sobre Semelhança de Triângulos: (UNESP) Um observador situado em um ponto o, localizado na margem de um rio, precisa determinar sua distância até um ponto p, localizado na outra margem, sem atravessar o rio. Para isso, marca, com estacas, outros pontos do lado da margem em que se encontra, de tal forma que p, o e B estão alinhados entre si, e p, A e C, também.
Além disso, é paralelo a
,
= 25 m,
= 40 m e
= 30 m, conforme figura.
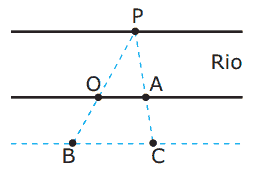
A distância, em metros, do observador em o até o ponto p é:
A) 30
B) 35
C) 40
D) 45
E) 50
Questão 02. (FUVEST-SP) O triângulo ABC tem altura h e base b (ver figura). Nele, está inscrito o retângulo DEFG, cuja base é o dobro da altura. Nessas condições, a altura do retângulo, em função de h e b, é dada pela fórmula
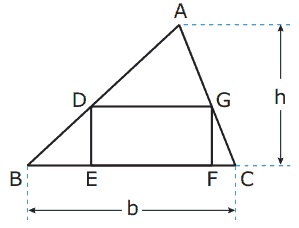
A)
B)
C)
D)
E)
Questão 03. (UFRN) Considerando-se as informações constantes no triângulo PQR (figura a seguir), pode-se concluir que a altura desse triângulo mede
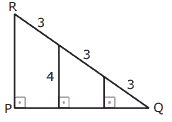
A) 5
B) 6
C) 7
D) 8
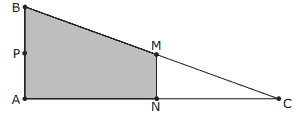
Questão 04 sobre Semelhança de Triângulos: (UNESP) Na figura, B é um ponto do segmento de reta , e os ângulos DÂB, D
E e B
E são retos.
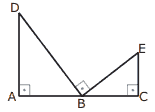
Se o segmento AD = 6 dm, o segmento AC = 11 dm e o segmento EC = 3 dm, as medidas possíveis de , em dm, são:
A) 4,5 e 6,5
B) 7,5 e 3,5
C) 8 e 3
D) 7 e 4
E) 9 e 2
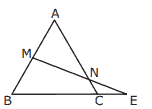
Questão 05. (Enem–2010) Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano.
Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto.
Nessas condições, a área a ser calçada corresponde:
A) à mesma área do triângulo AMC.
B) à mesma área do triângulo BNC.
C) à metade da área formada pelo triângulo ABC.
D) ao dobro da área do triângulo MNC.
E) ao triplo da área do triângulo MNC.
Questão 06. (Fatec-SP) Na figura a seguir, o triângulo ABC é retângulo e isósceles, e o retângulo nele inscrito tem lados que medem 4 cm e 2 cm.
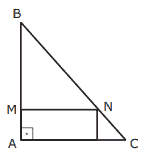
O perímetro do triângulo MBN é:
A) 8 cm.
B) 12 cm.
C) (8 + √2) cm.
D) (8 + 2√2) cm.
E) 4(2 + √2) cm.+
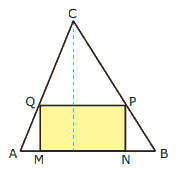
Questão 07 sobre Semelhança de Triângulos: (FUVEST-SP) No triângulo acutângulo ABC, a base AB mede 4 cm, e a altura relativa a essa base também mede 4 cm. MNPQ é um retângulo, cujos vértices M e N pertencem ao lado , p pertence ao lado
e Q, ao lado
. O perímetro desse retângulo, em cm, é:
A) 4
B) 8
C) 12
D) 14
E) 16
Questão 08. (Enem–2009) A rampa de um hospital tem, na sua parte mais elevada, uma altura de 2,2 metros. Um paciente, ao caminhar sobre a rampa, percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metro.
A distância, em metros, que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é:
A) 1,16 metro.
B) 3,0 metros.
C) 5,4 metros.
D) 5,6 metros.
E) 7,04 metros.
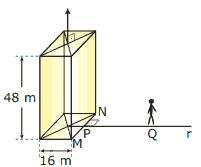
Questão 09. (UFF-RJ) Um prédio com a forma de um paralelepípedo retângulo tem 48 m de altura. No centro da cobertura desse prédio e perpendicularmente a essa cobertura, está instalado um para-raios. No ponto Q sobre a reta r – que passa pelo centro da base do prédio e é perpendicular ao segmento –, está um observador que avista somente uma parte do para-raios (ver a figura). A distância do chão aos olhos do observador é 1,8 m, e o segmento PQ = 61,6 m. O comprimento da parte do para-raios que o observador NÃO consegue avistar é:
A) 16 m.
B) 12 m.
C) 8 m.
D) 6 m.
E) 3 m.
Questão 10 sobre Semelhança de Triângulos: (AFA-SP) Na figura a seguir, o perímetro do triângulo equilátero ABC é 72 cm, M é o ponto médio de e
= 16 cm. Então, a medida do segmento
, em cm, é um sétimo de:
A) 48
B) 49
C) 50
D) 51

Gabarito com as respostas das 10 questões sobre Semelhança de Triângulos:
01. E;
02. D;
03. B;
04. E;
05. E;
06. E;
07. B;
08. D;
09. D;
10. A
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
