Questão 01 sobre Probabilidade e Estatística: (FGV-SP) Um conjunto de dados numéricos tem variância igual a zero.
Podemos concluir que:
A) a média também vale zero.
B) a mediana também vale zero.
C) a moda também vale zero.
D) o desvio padrão também vale zero.
E) todos os valores desse conjunto são iguais a zero.
Questão 02. (UFLA-MG–2006) A idade de uma árvore pode ser avaliada pela medida do diâmetro de seu tronco. A construção de diagramas indicando a distribuição em intervalos de classe para o diâmetro é uma forma de analisar a estrutura etária de uma população de árvores. O gráfico a seguir mostra a distribuição das classes de diâmetro para a espécie arbórea Xylopia aromatica.
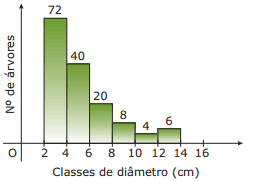
Considerando esses dados, quantas árvores possuem troncos com diâmetro não inferiores a 8 cm?
A) 8 árvores
B) 140 árvores
C) 4 árvores
D) 18 árvores
E) 10 árvores
Questão 03. (FGV-SP–2007) Quatro amigos calcularam a média e a mediana de suas alturas, tendo encontrado como resultados 1,72 m e 1,70 m, respectivamente.
A média entre as alturas do mais alto e do mais baixo, em metros, é igual a:
A) 1,70
B) 1,71
C) 1,72
D) 1,73
E) 1,74
Questão 04 sobre Probabilidade e Estatística: Vunesp. O gerente de uma loja de roupas, antes de fazer nova encomenda de calças jeans femininas, verificou qual foi a quantidade de calças vendidas no mês anterior para cada número (tamanho).
A distribuição de probabilidades referente aos números vendidos no mês anterior foi a seguinte:
| Número (tamanho) | 36 | 38 | 40 | 42 | 44 | 46 |
| Probabilidade | 0,12 | 0,22 | 0,30 | 0,20 | 0,11 | 0,05 |
Se o gerente fizer uma encomenda de 500 calças de acordo com as probabilidades de vendas dadas na tabela, as quantidades de calças encomendadas de número 40 ou menos, e de número superior a 40, serão, respectivamente:
a. 320 e 180.
b. 380 e 120.
c. 350 e 150.
d. 180 e 320.
e. 120 e 380.
Questão 05. UFPR – André, Beatriz e João resolveram usar duas moedas comuns, não viciadas, para decidir quem irá lavar a louça do jantar, lançando as duas moedas simultaneamente, uma única vez. Se aparecerem duas coroas, André lavará a louça; se aparecerem duas caras, Beatriz lavará a louça; e se aparecerem uma cara e uma coroa, João lavará a louça.
A probabilidade de que João venha a ser sorteado para lavar a louça é de:
a. 25%.
b. 27,5%.
c. 30%.
d. 33,3%.
e. 50%.
Questão 06. (Unimontes-MG–2008) Qual a média aritmética (Ma), a moda (Mo) e a mediana (Me), respectivamente, dos dados da tabela de frequências a seguir?
Idade dos alunos da 7ª A – Escola Gama – 2007
| Idade | Frequência |
| 13 14 15 16 | 3 2 4 1 |
| Total | 10 |
Fonte: SECRETARIA DA ESCOLA GAMA.
A) 14,5; 15; 14,3
B) 14,5; 15; 14,5
C) 14,3; 14,5; 15
D) 14,3; 15; 14,5
Questão 07 sobre Probabilidade e Estatística: (Enem–2009) A tabela mostra alguns dados da emissão de dióxido de carbono de uma fábrica em função do número de toneladas produzidas.
| Produção (em toneladas) | Emissão de dióxido de carbono (em partes por milhão – p.p.m.) |
| 1,1 | 2,14 |
| 1,2 | 2,30 |
| 1,3 | 2,46 |
| 1,4 | 2,64 |
| 1,5 | 2,83 |
| 1,6 | 3,03 |
| 1,7 | 3,25 |
| 1,8 | 3,48 |
| 1,9 | 3,73 |
| 2,0 | 4,00 |
Cadernos do Gestar II. Matemática TP3. Disponível em: <www.mec.gov.br>. Acesso em: 14 jul. 2009.
Os dados na tabela indicam que a taxa média de variação entre a emissão de dióxido de carbono (em p.p.m.) e a produção (em toneladas) é:
A) inferior a 0,18.
B) superior a 0,18 e inferior a 0,50.
C) superior a 0,50 e inferior a 1,50.
D) superior a 1,50 e inferior a 2,80.
E) superior a 2,80.
Questão 08. FGV-SP – Uma moeda é viciada de tal forma que os resultados possíveis, cara e coroa, são tais que a probabilidade de sair cara num lançamento é o triplo da de sair coroa.
a. Lançando-se uma vez a moeda, qual a probabilidade de sair cara?
b. Lançando-se três vezes a moeda, qual a probabilidade de sair exatamente uma cara?
Questão 09. Unesp – O mercado automobilístico brasileiro possui várias marcas de automóveis disponíveis aos consumidores. Para cinco dessas marcas (A, B, C, D e E), a matriz fornece a probabilidade de um proprietário de um carro de marca da linha i trocar para o carro de marca da coluna j, quando da compra de um carro novo. Os termos da diagonal principal dessa matriz fornecem as probabilidades de um proprietário permanecer com a mesma marca de carro na compra de um novo.
| A | B | C | D | E | |||||||||||
| A | B | C | D | E | ||||||||||||
| A | 0,6 | 0,1 | 0,2 | 0,1 | 0,0 | |||||||||||
| B | 0,3 | 0,5 | 0,0 | 0,1 | 0,1 | |||||||||||
| C | 0,2 | 0,2 | 0,4 | 0,1 | 0,1 | |||||||||||
| D | 0,3 | 0,2 | 0,2 | 0,3 | 0,0 | |||||||||||
| E | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 |
A probabilidade de um proprietário de um carro da marca B comprar um novo carro da marca C, após duas compras, é:
a. 0,25.
b. 0,24.
c. 0,20.
d. 0,09.
e. 0,00.
Questão 10 sobre Probabilidade e Estatística: Vunesp – O resultado de uma pesquisa realizada pelo Ipesp sobre o perfil dos fumantes e publicada pela revista Veja de 3/6/98 mostra que, num grupo de 1.000 pessoas, 17% fumam e, dentre os fumantes, 44% são mulheres. Se, nesse grupo de 1.000 pessoas, uma é escolhida ao acaso, a probabilidade de ela ser fumante e mulher é, aproximadamente:
a. 0,044
b. 0,075
c. 0,44
d. 0,0075
e. 0,0044

Gabarito com as respostas das listas de exercícios de Matemática sobre Probabilidade e Estatística:
01. D;
02. D;
03. E;
04. A;
05. E;
06. D;
07. D;
08. a. 75%
b.
09. D;
10. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
