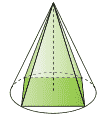
Questão 01 sobre Cilindro, Cone e Tetraedro: (UFRGS–2006) Duas esferas de raio r foram colocadas dentro de um cilindro circular reto com altura 4r, raio da base r e espessura desprezíveis, como na figura a seguir:

Nessas condições, a razão entre o volume do cilindro não ocupado pelas esferas e o volume das esferas é:
A)
B)
C)
D)
E)
Questão 02. (UFU-MG) Em um cubo de aresta a, considere um ponto Psituado em uma das arestas e que dista de um dos vértices do cubo. Chame de O o centro da esfera inscrita no cubo e de Q o ponto da esfera situado sobre o segmento OP.
A distância de P a Q é igual a:
A)
B)
C) (√5-2)
D) (√2-1)
Questão 03. (UFOP-MG) Uma pirâmide reta de base quadrada está inscrita num cone reto de raio da base 2√2 cm. A relação entre os volumes do cone e da pirâmide, nessa ordem, é:
A)
B)
C)
D)
Questão 04 sobre Cilindro, Cone e Tetraedro: (Fatec-SP) A interseção de um plano α com uma esfera de raio R é a base comum de dois cones circulares retos, como mostra a região sombreada da figura a seguir:
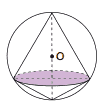
Se o volume de um dos cones é o dobro do volume do outro, a distância do plano α ao centro O é igual a:
A)
B)
C)
D)
E)
Questão 05. (UFU-MG) Considere que cada vértice de um cubo de aresta 1 cm é também o centro de uma esfera de raio 1 2 cm. O volume da região do espaço interna ao cubo e externa às oito esferas é igual a:
A) cm3.
B) cm3.
C) cm3.
D) cm3.
Questão 06. (UFMG) A razão entre as áreas totais de um cubo e do cilindro reto nele inscrito, nessa ordem, é:
A)
B)
C)
D)
E)
Questão 07 sobre Cilindro, Cone e Tetraedro: (Mackenzie-SP) Seja 36p o volume de uma esfera circunscrita a um cubo. Então, a razão entre o volume da esfera e o volume do cubo é:
A)
B)
C)
D)
E) √3π
Questão 08. (UFPE) Indique o valor da área lateral, em cm2, do sólido cujos vértices são os centros de simetria das faces de um cubo de aresta medindo L cm.
A) L√3
B) L2√3
C) L2√2
D) 3L2
E) 5L2
Questão 09. (CEFET-MG–2010) Um pilão de madeira, apoiado sobre hastes de metal, no formato de um cone circular reto de base com centro em A, foi esculpido por um artesão, conforme a figura.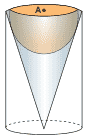
Para garantir uma boa proporcionalidade, a cuia do pilão foi esculpida na forma de uma semiesfera tangente ao cone, de maneira que o seu centro coincidisse com o ponto A. Sabendo-se que o pilão ficou com altura de √3 m e o cone, com raio da base igual a 1 m, o volume de madeira contido na peça, em m3, é:
A)
B)
C)
D)
E) √3x
Questão 10 sobre Cilindro, Cone e Tetraedro: (UFMG–2006) Nesta figura, estão representados o cubo ABCDEFGH e o prisma ACRPQO.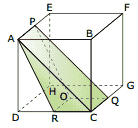
Sabe-se que:
I) P, Q e R são, respectivamente, os pontos médios das arestas AE, CG e CD.
II) o ponto O é o centro da face CDGH.
III) o volume do prisma ACRPQO é 24 cm3.
Então, é CORRETO afirmar que o comprimento de cada aresta desse cubo é:
A) 43√2 cm.
B) 23√3 cm.
C) 43√3 cm.
D) 23√2 cm.
Questão 11. (PUC-SP) Um cone circular reto, cujo raio da base é 3 cm, está inscrito em uma esfera de raio 5 cm, conforme mostra a figura a seguir: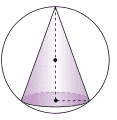
O volume do cone corresponde a que porcentagem do volume da esfera?
A) 26,4%
B) 21,4%
C) 19,5%
D) 18,6%
E) 16,2%
Questão 12. (PUC-SP) Uma pirâmide quadrangular regular é inscrita num cubo de aresta a. A área total da pirâmide é igual a:
A) a2
B) a2√5
C) a2(√5 + 1)
D) a2(2 + √5)
E) a2(5 + √5)
Questão 13 sobre Cilindro, Cone e Tetraedro: (PUC-SP–2006) De um cristal de rocha, com o formato de uma esfera, foi lapidada uma joia na forma de um octaedro regular, como mostra a figura a seguir: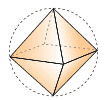
Se tal joia tem 9√2 cm3 de volume, quantos centímetros cúbicos de rocha foram retirados do cristal original para lapidá-la? Use: p = 3
A) 36√2
B) 32√2
C) 24√2
D) 18√2
E) 12√2
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista com 13 exercícios de matemática sobre Cilindro, Cone e Tetraedro:
01. D;
02. B;
03. C;
04. C;
05. C;
06. C;
07. A;
08. B;
09. A;
10. C;
11. E;
12. C;
13. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
