Questão 01 sobre Cones Geometria: (PUC RS) O raio da base de um cone circular reto e a aresta da base de uma pirâmide quadrangular regular têm mesma medida. Sabendo que suas alturas medem 4 cm, então a razão entre o volume do cone e o da pirâmide é:
A) 1
B) 4
C)
D) π
E) 3π
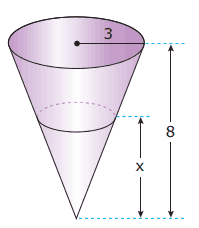
Questão 02. (FUVEST-SP) Um copo tem a forma de um cone com altura 8 cm e raio da base 3 cm. Queremos enchê-lo com quantidades iguais de suco e de água. Para que isso seja possível, a altura x atingida pelo primeiro líquido colocado deve ser:
A) cm.
B) 6 cm.
C) 4 cm.
D) 4√3 cm.
E) 4 cm.
Questão 03. (UFJF-MG) O vinho contido em uma jarra cilíndrica será servido em cálices em forma de cone. A altura de cada cálice é da altura da jarra e o diâmetro da circunferência que forma a sua borda é
do diâmetro da base da jarra.
DETERMINE o número de cálices necessários para que o vinho seja todo servido de uma só vez.
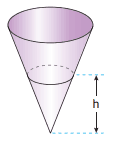
Questão 04 sobre Cones Geometria: (UFMG) Um tanque de água tem a forma de um cone circular reto, com seu vértice apontando para baixo. O raio do topo é igual a 9 m e a altura do tanque é de 27 m. Pode-se afirmar que o volume V da água no tanque, como função da altura h da água, é:
A)
B)
C)
D) 3πh3
E) 9πh3
Questão 05. (UFSC) A geratriz de um cone equilátero mede 2√3 cm. CALCULE a área da seção meridiana do cone, em cm2, e MULTIPLIQUE o resultado por √3.
Questão 06. (PUC-Campinas-SP) Considere o triângulo ABC, representado na figura a seguir, no qual BC = 6 + 6√3 cm.
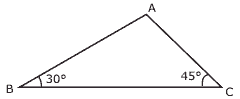
Por uma rotação de 360° em torno do lado BC, obtém-se um sólido que servirá de modelo para a construção de um balão. O volume desse modelo, em centímetros cúbicos, será:
A) (√3+ 3)72π
B) (√3 + 1)72π
C) (√3 + 3)36π
D) ( √3 + 1)36π
E) (√3 + 3)24π
Questão 07 sobre Cones Geometria: (UFMG) Um cone é construído de forma que:
I) sua base é um círculo inscrito em uma face de um cubo de lado a.
II) seu vértice coincide com um dos vértices do cubo localizado na face oposta àquela em que se encontra a sua base.
Dessa maneira, o volume do cone é de:
A)
B)
C)
D)
Questão 08. (UFJF-MG–2008) Fernando utiliza um recipiente, em forma de um cone circular reto, para encher com água um aquário em forma de um paralelepípedo retângulo.
As dimensões do cone são: 20 cm de diâmetro de base e 20 cm de altura, e as do aquário são: 120 cm, 50 cm e 40 cm, conforme ilustração a seguir.
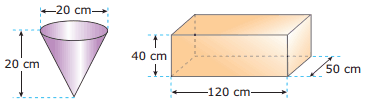
Cada vez que Fernando enche o recipiente na torneira do jardim, ele derrama 10% de seu conteúdo no caminho e despeja o restante no aquário. Estando o aquário inicialmente vazio, qual é o número mínimo de vezes que Fernando deverá encher o recipiente na torneira para que a água despejada no aquário atinja de sua capacidade?
Questão 09. (Enem–2009) Um vasilhame na forma de um cilindro circular reto de raio da base de 5 cm e altura de 30 cm está parcialmente ocupado por 625π cm3 de álcool. Suponha que sobre o vasilhame seja fixado um funil na forma de um cone circular reto de raio da base de 5 cm e altura de 6 cm, conforme ilustra a figura 1. O conjunto, como mostra a figura 2, é virado para baixo, sendo H a distância da superfície do álcool até o fundo do vasilhame. Volume do cone: Vcone
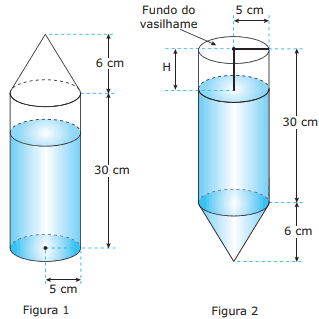
Considerando-se essas informações, qual é o valor da distância H?
A) 5 cm
B) 7 cm
C) 8 cm
D) 12 cm
E) 18 cm
Questão 10 sobre Cones Geometria: (Enem–2009) Uma empresa precisa comprar uma tampa para o seu reservatório, que tem a forma de um tronco de cone circular reto, conforme mostrado na figura a seguir:
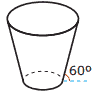
Considere que a base do reservatório tenha raio r = 2√3 m e que sua lateral faça um ângulo de 60° com o solo. Se a altura do reservatório é 12 m, a tampa a ser comprada deverá cobrir uma área de:
A) 12π m2.
B) 108π m2.
C) (12 + 2 √3 )2 π m2.
D) 300p m2.
E) (24 + 2√3)2 m2
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista de exercícios de matemática sobre Cones Geometria:
01. D;
02. E;
03. 27;
04. A;
05. 9;
06. B;
07. B;
08. 26;
09. B;
10. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
