Questão 01 sobre Matrizes: (FGV-SP–2009) As matrizes A, B, e C são quadradas
de ordem 3, e O é a matriz nula, também de ordem 3. Assinale a alternativa CORRETA.
A) (A – B).C = A.C – B.C
B) A.C = C.A
C) (A + B).(A – B) = A2 – B2
D) (B + C)2 = B2 + 2.B.C + C2
E) Se A.B = O, então, A = O ou B = O.
Questão 02. (UFU-MG) Seja A uma matriz de terceira ordem com elementos reais. Sabendo-se que A , conclui-se que –1, 4 e 2 são os elementos da:
A) diagonal da transposta de A.
B) primeira coluna da transposta de A.
C) primeira linha da transposta de A.
D) última linha da transposta de A
Questão 03. (UFU-MG) Se A, B e C são matrizes 4×3, 3×4 e 4×2, respectivamente, então a transposta do produto A.B.C é uma matriz do tipo:
A) 4×2
B) 2×4
C) 3×2
D) 1×3
E) Nesta ordem o produto não é definido.
Questão 04 sobre Matrizes: (Fatec-SP) Sabe-se que as ordens das matrizes A, B e C são, respectivamente, 3xr, 3xs e 2xt. Se a matriz (A – B).C é de ordem 3×4, então r + s + t é igual a:
A) 6
B) 8
C) 10
D) 12
E) 14
Questão 05. (UNIRIO-RJ) Considere as matrizes A = , B =
e C = [2 1 3]. A adição da transposta de A com o produto de B por C é:
A) impossível de se efetuar, pois não existe o produto de B por C.
B) impossível de se efetuar, pois as matrizes são todas de tipos diferentes.
C) impossível de se efetuar, pois não existe a soma da transposta de A com o produto de B por C.
D) possível de se efetuar, e seu resultado é do tipo 2×3.
E) possível de se efetuar, e seu resultado é do tipo 3×2.
Questão 06. (Unimontes-MG) Um construtor tem contratos para construir 2 estilos de casa: moderno e colonial. A quantidade de material empregado em cada tipo de casa é dada pela matriz:
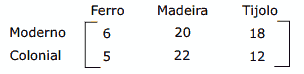
Suponha que o construtor vá construir 2 casas do tipo moderno e 3 do tipo colonial. Se os preços por unidade de ferro, madeira e tijolo são, respectivamente, R$15,00, R$8,00 e R$10,00, então o custo total do material empregado é igual a:
A) R$ 1 923,00.
B) R$ 1 602,00.
C) R$ 1 973,00.
D) R$ 1 932,00.
Questão 07 sobre Matrizes: (FGV-SP) A matriz A = é inversa de B =
. Nessas condições, podemos afirmar que a soma x + y vale:
A) –1
B) –2
C) –3
D) –4
E) –5
Questão 08. (PUC-SP) Sendo A e B matrizes inversíveis de mesma ordem e X uma matriz tal que (X.A)t = B, então:
A) X = A-1.Bt
B) X = Bt.A-1
C) X = (B.A)t
D) X = (A.B)t
E) N.d.a.
Questão 09. (FGV-SP) No que se refere à solução da equação A.X = B em que A e B são matrizes quadradas de ordem 3, pode-se dizer que:
A) a equação pode não ter solução.
B) a equação nunca tem solução.
C) a equação tem sempre uma solução que é X = .
D) a equação tem sempre uma solução que é X = B.A-1.
E) a equação tem sempre uma solução que é X = A-1.B.
Questão 10 sobre Matrizes: (UFV-MG) Considerando a matriz A3x3, cujo termo geral é dado por a xy = (–1)x+Y, é CORRETO afirmar que:
A) A = –At
B) A é inversível.
C) a11 + a22 + a33 = 0
D) axy = cos [(x + y)π]
E) a11 + a21 + a31 = 0
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos melhores exercícios de matemática sobre Matrizes:
01. A;
02. C;
03. B;
04. B;
05. D;
06. C;
07. C;
08. B;
09. A;
10. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
