10 Exercícios sobre as Leis dos Senos e Cossenos

Questão 01 sobre Leis dos Senos e Cossenos: (PUC-SP) Sejam a, b e c as medidas dos lados de um triângulo ABC. Então, se:

A) a² < b² + c², o triângulo ABC é retângulo.
B) a² = b² + c², o lado a mede a soma das medidas de b e c.
C) a² > b² + c², o ângulo oposto ao lado que mede a é obtuso.
D) b² = a² + c², a é a hipotenusa, e b e c são catetos.
E) Nenhuma das anteriores é correta.

Questão 02. (UNESP–2009) Paulo e Marta estão brincando de jogar dardos. O alvo é um disco circular de centro O. Paulo joga um dardo, que atinge o alvo num ponto que vamos denotar por P; em seguida, Marta joga outro dardo, que atinge um ponto denotado por M, conforme figura.

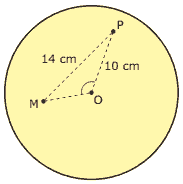
Sabendo-se que a distância do ponto P ao centro O do alvo é  = 10 cm, que a distância de P a M é PM = 14 cm e que o ângulo PÔM mede 120º, a distância, em centímetros, do ponto M ao centro O é:

A) 12
B) 9
C) 8
D) 6
E) 5

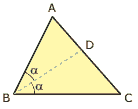
Questão 03. (UFBA) Na figura a seguir, AB = 3 cm, BC = 4 cm e  = 60°. AD é, aproximadamente, igual a:

A) 1,2 cm.
B) 1,4 cm.
C) 1,54 cm
D) 1,8 cm.
E) 2,04 cm.

Questão 04 sobre Leis dos Senos e Cossenos: (Cesesp-PE) “Com três segmentos de comprimentos iguais a 10 cm, 12 cm e 23 cm,:

A) é possível formar apenas um triângulo retângulo.”
B) é possível formar apenas um triângulo obtusângulo.”
C) é possível formar apenas um triângulo acutângulo.”
D) não é possível formar um triângulo.”
E) é possível formar qualquer um dos triângulos: retângulo, acutângulo ou obtusângulo.”

Questão 05. (FEI-SP) Assinale a alternativa FALSA quanto ao tipo de triângulo, dados os lados a, b e c.

A) Se a = 13, b = 5, c = 12, o triângulo é retângulo.
B) Se a = 18, b = 5, c = 12, é um triângulo.
C) Se a = 5, b = 5, c = 5, o triângulo é equilátero.
D) Se a = 5, b = 7, c = 7, o triângulo é isósceles.
E) Se a = 1, b = 2, c = 3, não é triângulo.

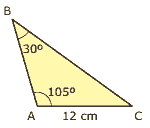
Questão 06. (Mackenzie-SP) Três ilhas A, B e C aparecem num mapa, em escala 1:10 000, como na figura. Das alternativas, a que MELHOR se aproxima de distância entre as ilhas A e B é:

A) 2,3 km.
B) 2,1 km.
C) 1,9 km.
D) 1,4 km.
E) 1,7 km.

Questão 07 sobre Leis dos Senos e Cossenos: (ITA-SP) Num triângulo ABC, BC = 4 cm, o ângulo C mede 30° e a projeção do lado  sobre  mede 2,5 cm. O comprimento da mediana que sai do vértice A mede:

A) 1 cm.
B) √2 cm.
C) 0,9 cm.
D) √3 cm.
E) 2 cm.

Questão 08. (Unifor-CE) Um terreno de forma triangular tem frentes de 10 m e 20 m, em ruas que formam, entre si, um ângulo de 120º. A medida do terceiro lado do terreno, em metros, é:

A) 10√5
B) 10√6
C) 10√7
D) 26
E) 20√2

Questão 09. (Cesgranrio) Se 4 cm, 5 cm e 6 cm são as medidas dos lados de um triângulo, então o cosseno do seu menor ângulo vale:

A)

B)

C)

D)

E)

Questão 10 sobre Leis dos Senos e Cossenos: (ENEM) Em escolas infantis, é comum encontrar um brinquedo, chamado escorregador, constituído de uma superfície plana inclinada e lisa (rampa), por onde as crianças deslizam, e de uma escada. No pátio da escolinha Casa Feliz, há um escorregador, apoiado em um piso plano e horizontal, cuja escada tem 8 degraus espaçados de 25 cm e forma um ângulo de 60º com o piso.

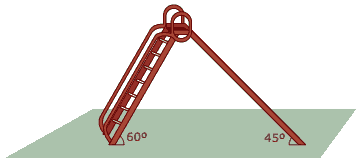
O comprimento da rampa, sabendo-se que ela forma com o chão um ângulo de 45º, é de:
A) √3 m.
B) √6 m.
C) 2√2 m.
D) 2√3 m.
E) 2√6 m.

🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.

Gabarito com as respostas dos exercícios de Matemática sobre as Leis dos Senos e Cossenos:

01. C;

02. D;

03. C;

04. D;

05. B;

06. E;

07. A;

08. C;

09. C;

10. B

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína