Questão 01 sobre Geometria Plana: Modelo enem. Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
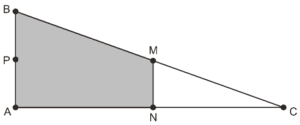
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calcada corresponde
a) a mesma área do triângulo AMC.
b) a mesma área do triângulo BNC.
c) a metade da área formada pelo triângulo ABC.
d) ao dobro da área do triângulo MNC.
e) ao triplo da área do triângulo MNC.
Questão 02. Modelo enem. A ideia de usar rolos circulares para deslocar objetos pesados provavelmente surgiu com os antigos egípcios ao construírem as pirâmides.
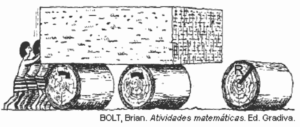
Representando por R o raio da base dos rolos cilíndricos, em metros, a expressão do deslocamento horizontal y do bloco de pedra em função de R, após o rolo ter dado uma volta completa sem deslizar, é:
a) y = R.
b) y = 2R.
c) y = πR.
d) y = 2πR.
e) y = 4πR.
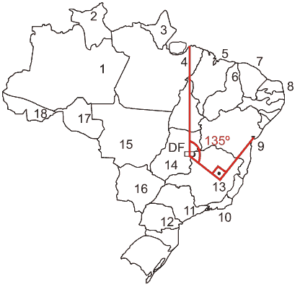
Questão 03. Modelo enem. Rotas aéreas são como pontes que ligam cidades, estados ou países. O mapa a seguir mostra os estados brasileiros e a localização de algumas capitais identificadas pelos números. Considere que a direção seguida por um avião AI que partiu de Brasília – DF, sem escalas, para Belém, no Pará, seja um segmento de reta com extremidades em DF e em 4.
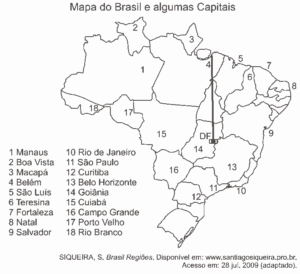
Suponha que um passageiro de nome Carlos pegou um avião AII, que seguiu a direção que forma um ângulo de 135o graus no sentido horário com a rota Brasília – Belém e pousou em alguma das capitais brasileiras. Ao desembarcar, Carlos fez uma conexão e embarcou em um avião AIII, que seguiu a direção que forma um ângulo reto, no sentido anti-horário, com a direção seguida pelo avião AII ao partir de Brasília-DF.
Considerando que a direção seguida por um avião é sempre dada pela semirreta com origem na cidade de partida e que passa pela cidade destino do avião, pela descrição dada, o passageiro Carlos fez uma conexão em:
a) Belo Horizonte, e em seguida embarcou para Curitiba.
b) Belo Horizonte, e em seguida embarcou para Salvador.
c) Boa Vista, e em seguida embarcou para Porto Velho.
d) Goiânia, e em seguida embarcou para o Rio de Janeiro.
e) Goiânia, e em seguida embarcou para Manaus.
Questão 04 sobre Geometria Plana: Modelo enem. A fotografia mostra uma turista aparentemente beijando a esfinge de Gizé, no Egito. A figura a seguir mostra como, na verdade, foram posicionadas a câmera fotográfica, a turista e a esfinge.
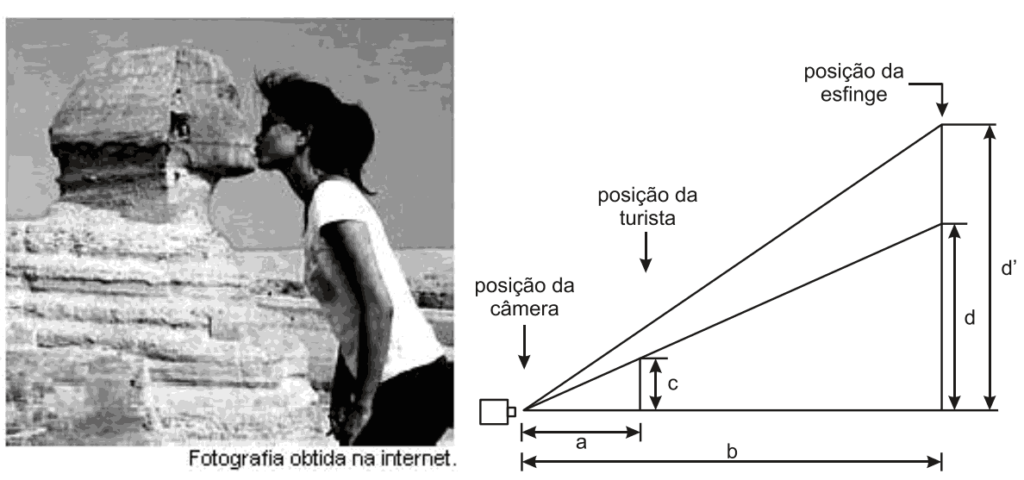
Medindo-se com uma régua diretamente na fotografia, verifica-se que a medida do queixo até o alto da cabeça da turista é igual a ![]() da medida do queixo da esfinge até o alto da sua cabeça. Considere que essas medidas na realidade são representadas por d e d’, respectivamente, que a distância da esfinge à lente da câmera fotográfica, localizada no plano horizontal do queixo da turista e da esfinge, é representada por b, e que a distância da turista à mesma lente, por a. A razão entre b e a será dada por
da medida do queixo da esfinge até o alto da sua cabeça. Considere que essas medidas na realidade são representadas por d e d’, respectivamente, que a distância da esfinge à lente da câmera fotográfica, localizada no plano horizontal do queixo da turista e da esfinge, é representada por b, e que a distância da turista à mesma lente, por a. A razão entre b e a será dada por

Questão 05. Modelo enem. A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metro.
A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é:
a) 1,16 metros.
b) 3,0 metros.
c) 5,4 metros.
d) 5,6 metros.
e) 7,04 metros.
Questão 06. Modelo enem.
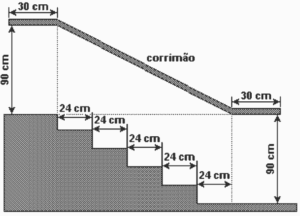
Na figura acima, que representa o projeto de uma escada com 5 degraus de mesma altura, o comprimento total do corrimão é igual a:
a) 1,8 m.
b) 1,9 m.
c) 2,0 m.
d) 2,1m.
e) 2,2 m.
Questão 07 sobre Geometria Plana: Modelo Enem. Quatro estações distribuidoras de energia A, B, C e D estão dispostas como vértices de um quadrado de 40km de lado. Deseja-se construir uma estação central que seja ao mesmo tempo equidistante das estações A e B e da estrada (reta) que liga as estações C e D.
A nova estação deve ser localizada:
a) no centro do quadrado.
b) na perpendicular à estrada que liga C e D passando por seu ponto médio, a 15km dessa estrada.
c) na perpendicular à estrada que liga C e D passando por seu ponto médio, a 25km dessa estrada.
d) no vértice de um triângulo equilátero de base AB, oposto a essa base.
e) no ponto médio da estrada que liga as estações A e B.
Questão 08. Modelo Enem. As cidades de Quito e Cingapura encontram-se próximas à linha do equador e em pontos diametralmente postos no globo terrestre. Considerando o raio da Terra igual a 6370km, pode-se afirmar que um avião saindo de Quito, voando em média 800km/h, descontando as paradas de escala, chega a Cingapura em aproximadamente
a) 16 horas.
b) 20 horas.
c) 25 horas.
d) 32 horas.
e) 36 horas.
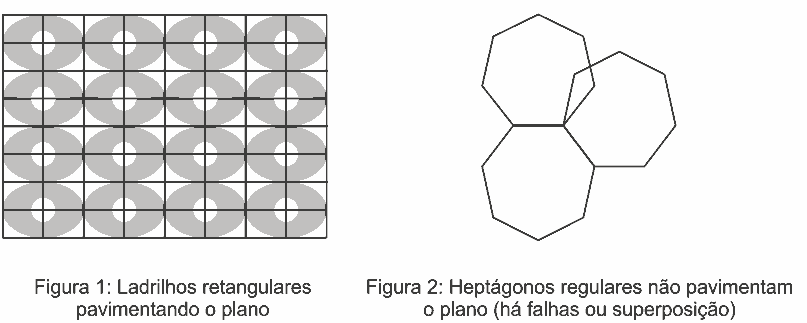
Questão 09. Modelo Enem. Na construção civil, é muito comum a utilização de ladrilhos ou azulejos com a forma de polígonos para o revestimento de pisos ou paredes. Entretanto, não são todas as combinações de polígonos que se prestam a pavimentar uma superfície plana, sem que haja falhas ou superposições de ladrilhos, como ilustram as figuras:
A tabela traz uma relação de alguns polígonos regulares, com as respectivas medidas de seus ângulos internos.
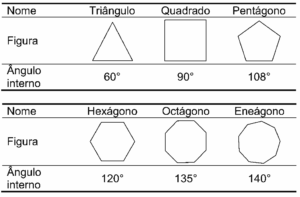
Se um arquiteto deseja utilizar uma combinação de dois tipos diferentes de ladrilhos entre os polígonos da tabela, sendo um deles octogonal, o outro tipo escolhido deverá ter a forma de um:
a) triângulo.
b) quadrado.
c) pentágono.
d) hexágono.
e) eneágono.
Questão 10 sobre Geometria Plana: Modelo Enem. Um marceneiro deseja construir uma escada trapezoidal com 5 degraus, de forma que o mais baixo e o mais alto tenham larguras respectivamente iguais a 60 cm e a 30 cm, conforme a figura:
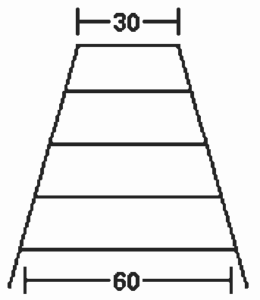
Os degraus serão obtidos cortando-se uma peça linear de madeira cujo comprimento mínimo, em cm, deve ser:
a) 144.
b) 180.
c) 210.
d) 225.
e) 240.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas das 10 questões de matemática sobre Geometria Plana:
01. E
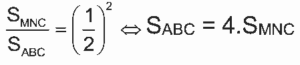
SABMN= SABC – SMNC =
SABMN = 4.SMNC – SMNC
SABMN = 3. SCMN (TRIPLO)
02. E
Deslocamento do rolo em relação ao solo: 2π.R .
Deslocamento do bloco em relação ao rolo: 2π.R .
Deslocamento do bloco em relação ao solo: 4π.R .
03. B
De acordo com o desenho a seguir, Belo Horizonte e Salvador.
04. D
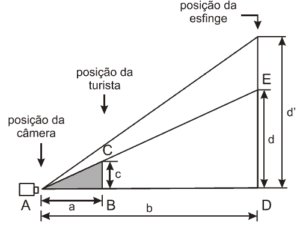
Na figura o ∆BC ~ ∆ADE logo
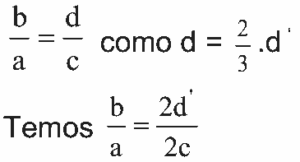
05. D
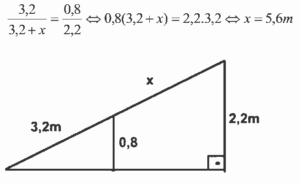
06. D
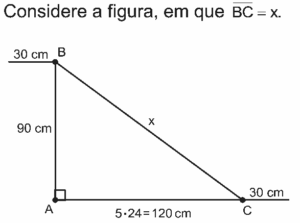
Aplicando o Teorema de Pitágoras no triângulo ABC, obtemos
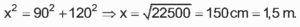
portanto, o comprimento total do corrimão é 1,5 + 2 x 0,3 = 2,1m.
07. C
Considere a figura abaixo, em que P é o ponto onde deverá ser construída a estação.
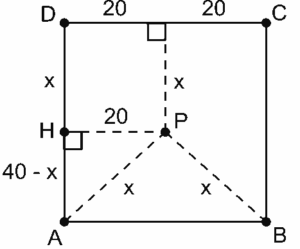
Aplicando o Teorema de Pitágoras no triângulo APH, obtemos

Por conseguinte, a nova estação deverá ser construída na perpendicular à estrada que liga C e D passando por seu ponto médio, a 25km dessa estrada.
08. C
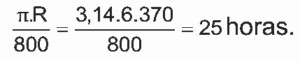
09. B
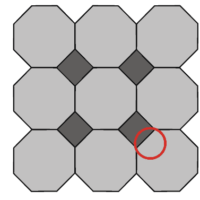
Cada ângulo interno do octógono regular mede 135° e cada ângulo interno do quadrado mede 90°. Somando 135° + 135° + 90° = 360°. Portanto, o polígono pedido é o quadrado.
10.D
Duplicando a figura dada, como na figura a seguir, podemos observar 5 degraus de 90 cm cada.
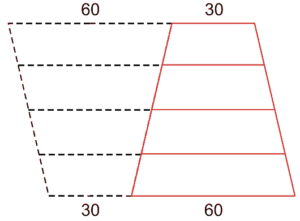
Logo a soma dos comprimentos dos degraus da escada é 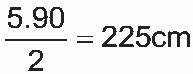 . Portanto, será necessária uma peça linear de no mínimo 225 cm.
. Portanto, será necessária uma peça linear de no mínimo 225 cm.
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
