10 Atividades sobre Transformações Trigonométricas

Questão 01 sobre Transformações Trigonométricas: (AFA) O valor da expressão cos 15° + sen 105° é:

Questão 02. (FEI) Se cos x = 0,8 e 0 < x < , então o valor de sen 2x é:

a) 0,6.
b) 0,8.
c) 0,96.
d) 0,36.
e) 0,49.

Questão 03. (UFES) Sabendo que tg x = √2 – 1, calcular tg 2x.

Questão 04 sobre Transformações Trigonométricas: (Fuvest)

a) Calcule sen15°.
b) Calcule a área do polígono regular de 24 lados inscrito no círculo de raio 1.

Questão 05. (Unifesp) A expressão sen(x _ y) cos y + cos(x _ y) sen y é equivalente a:

a) sen (2x + y).
b) cos 2x.
c) sen x.
d) sen 2x.
e) cos (2x + 2y).

Questão 06. (FGV) A função f(x) = 16 sen x cos x assume valor máximo igual a:

a) 16.
b) 12.
c) 10.
d) 8.
e) 4.

Questão 07 sobre Transformações Trigonométricas: (UFG) A figura a seguir representa uma quadra retangular inscrita num terreno semicircular cujo raio mede 10 m.

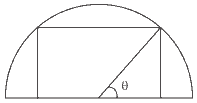
Nessas condições:
a) expresse a área da quadra em função do ângulo α;
b) determine as dimensões da quadra que possui área máxima.

Questão 08. (Fuvest) Resolva em R a equação:

cos x sen 2x = (sen x) (1 + cos 2x)

Questão 09. (UERJ) Considere o ângulo segundo o qual um observador vê uma torre. Esse ângulo duplica quando ele se aproxima 160 m e quadruplica quando ele se aproxima mais 100 m, como mostra o esquema abaixo:

A altura da torre, em metros, equivale a:
a) 96.
b) 98.
c) 100.
d) 102.

Questão 10 sobre Transformações Trigonométricas: (UERJ) Alguns cálculos matemáticos ficam mais simples quando usamos identidades, tais como:

a² – b² = (a + b)(a _ b)

a² + 2ab + b² = (a + b)²

a³ + b³ = (a + b) (a² _ ab + b²)

Considerando essas identidades, calcule os valores numéricos racionais mais simples das expressões:

a) (57,62)² _ (42,38)²;

b) cos⁶ 15° + sen⁶ 15°.

🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.

Gabarito com as respostas das 10 atividades de matemática sobre as Transformações Trigonométricas:

01. c;
02. c;
03. 1;

04. a)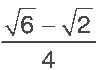

b)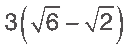

05. c;
06. d;
07. a) 100 sen 2θ;
08. S = R;

09. a;

10. a) 1.524
b) 13/16

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína