10 Exercícios sobre os Conceitos Básicos de Funções Matemáticas

Questão 01 sobre Conceitos Básicos de Funções Matemáticas: (UFPA) Sejam os conjuntos A = {1, 2} e B = {0, 1, 2}. Qual das afirmativas a seguir é VERDADEIRA?

A) f: x → 2x é uma função de A em B.
B) f: x → x + 1 é uma função de A em B.
C) f: x → x2 – 3x + 2 é uma função de A em B.
D) f: x → x2 – x é uma função de B em A.
E) f: x → x – 1 é uma função de B em A.

Questão 02. (UFMG) Uma função f: R → R é tal que f(5x) = 5 f(x) para todo número real x. Se f(25) = 75, então o valor de f(1) é:

A) 3
B) 5
C) 15
D) 25
E) 45

Questão 03. (UFMG) Das figuras a seguir, a ÚNICA que representa o gráfico de uma função real y = f(x), x ∈ [a, b], é:

Questão 04 sobre Conceitos Básicos de Funções Matemáticas: (UFMG) Seja f(x) = 3^2x. Sabendo-se que f(x + h) = 9 f(x) para todo valor real de x, o valor de h é:

A) 0
B) 1
C) 2
D) 3
E) 4

Questão 05. (UFMG) Se f é uma função tal que f(1) = 3 e f(x + y) = f(x) + f(y) para qualquer x e y reais, então f(2) é igual a:

A) 1
B) 2
C) 3
D) 6
E) 8

Questão 06. (UFMG) Observe a figura a seguir. Nela, estão representados o ponto A, cuja abscissa é 1, e o ponto B, cuja ordenada é 5. Esses dois pontos pertencem ao gráfico da função f(x) = (x + 1)(x3 + ax + b), em que a e b são números reais. Assim, o valor de f(4) é :

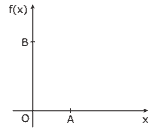
A) 65
B) 115
C) 170
D) 225

Questão 07 sobre Conceitos Básicos de Funções Matemáticas: (UNESP) Uma pessoa parte de carro de uma cidade X com destino a uma cidade Y. Em cada instante t (em horas), a distância que falta percorrer até o destino é dada, em dezenas de quilômetros, pela função D, definida por:

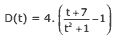
Considerando o percurso da cidade X até a cidade Y, a distância, em média, por hora, que o carro percorreu foi:

A) 40 km.
B) 60 km.
C) 80 km.
D) 100 km.
E) 120 km.

Questão 08. (Enem–2009) A suspeita de que haveria uma relação causal entre tabagismo e câncer de pulmão foi levantada pela primeira vez a partir de observações clínicas. Para testar essa possível associação, foram conduzidos inúmeros estudos epidemiológicos. Entre esses, houve o estudo do número de casos de câncer em relação ao número de cigarros consumidos por dia, cujos resultados são mostrados no gráfico a seguir:

Casos de câncer pulmonar dado o número de cigarros consumidos diariamente

Centers of Disease Control and Prevention CDC-EIS. Summer Course, 1992 (Adaptação).

De acordo com as informações do gráfico:
A) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas inversamente proporcionais.

B) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas que não se relacionam.

C) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas diretamente proporcionais.

D) uma pessoa não fumante certamente nunca será diagnosticada com câncer de pulmão.

E) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas que estão relacionadas, mas sem proporcionalidade.

Questão 09. (Enem–2010) Nos processos industriais, como na indústria de cerâmica, é necessário o uso de fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo de elevação dessa temperatura deve ser controlado, para garantir a qualidade do produto final e a economia no processo. Em uma indústria de  cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função:

em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado. Uma peça deve ser colocada nesse forno quando a temperatura for 48 ºC e retirada quando a temperatura for 200 ºC.

O tempo de permanência dessa peça no forno é, em minutos, igual a:
A) 100
B) 108
C) 128
D) 130
E) 150

Questão 10 sobre Conceitos Básicos de Funções Matemáticas: (Enem–2010) Um laticínio possui dois reservatórios de leite. Cada reservatório é abastecido por uma torneira acoplada a um tanque resfriado. O volume, em  litros, desses reservatórios depende da quantidade inicial de leite no reservatório e do tempo t, em horas, em que as duas torneiras ficam abertas. Os volumes dos reservatórios são dados pelas funções V1(t) = 250t3 – 100t + 3 000 e V2(t) = 150t3 + 69t + 3 000.

Depois de aberta cada torneira, o volume de leite de um reservatório é igual ao do outro no instante t = 0 e, também, no tempo t igual a:
A) 1,3 h.
B) 1,69 h.
C) 10,0 h.
D) 13,0 h.
E) 16,9 h.

🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.

Gabarito com as respostas dos melhores exercícios sobre Conceitos Básicos de Funções Matemáticas:

01. C;

02. A;

03. E;

04. B;

05. D;

06. D;

07. C;

08. E;

09. D;

10. A

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína