Questão 01 sobre Parábola, Hipérbole e Elipse: PUC-RJ – O número de pontos de intersecção das duas parábolas y = x2 e y = 2x2 – 1 é:
a) 0
b) 1
c) 2
d) 3
e) 4
Questão 02. UFMG – A reta r é paralela à reta de equação 3x – y – 10 = 0. Um dos pontos de interseção de r com a parábola de equação y = x2 – 4 tem abscissa 1.
A equação de r é:
a) 3x – y + 6 = 0
b) x – 3y – 10 = 0
c) 3x – y – 6 = 0
d) x + 3y + 8 = 0
Questão 03. Unifor-CE – Na figura abaixo tem-se o gráfico da função quadrática definida por y = ax2 + bx + c.
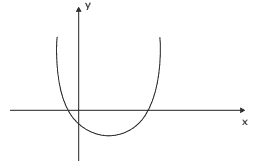
Se S e P são, respectivamente, a soma e o produto das raízes dessa função, e ∆ = b2 – 4ac, então:
a) ∆ < 0, S > 0 e P > 0
b) ∆ = 0, S = 0 e P < 0
c) ∆ > 0, S < 0 e P < 0
d) ∆ > 0, S > 0 e P < 0
e) ∆ > 0, S = 0 e P > 0
Questão 04 sobre Parábola, Hipérbole e Elipse: U. Uberaba-MG – Se o gráfico abaixo representa a parábola y = ax2 + bx + c, podemos afirmar que:
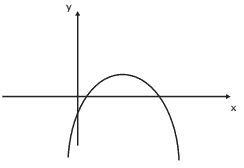
a) a > 0, b < 0 e c < 0.
b) a < 0, b > 0 e c > 0.
c) a < 0, b > 0 e c < 0.
d) a < 0, b < 0 e c < 0.
Questão 05. U. Caxias do Sul-RS – Em uma experiência de laboratório um estudante de Biologia coletou os seguintes dados:
| t (tempo em horas) | s(t) |
| 1 | 1 |
| 2 | 1,5 |
| 3 | 4 |
Assumindo que os dados podem ser representados por um gráfico que é uma parábola, o valor de s(t), uma hora e meia após o início do experimento, é:
a) 1
b) 1,5
c) 2,4
d) 2,5
e) 3
Questão 06. UFCE – A área do quadrilátero cujos vértices são as interseções da elipse 9x2 + 25y2 = 225 com os eixos coordenados é igual, em unidades de área, a:
a) 30
b) 32
c) 34
d) 36
Questão 07 sobre Parábola, Hipérbole e Elipse: ITA-SP – Seja o ponto A = (r, 0), r > 0. O lugar geométrico dos pontos P = (x, y) tais que é de 3r2 a diferença entre o quadrado da distância de P a A e o dobro do quadrado da distância de P à reta y = –r, é:
a) uma circunferência centrada em (r, –2r) com raio r.
b) uma elipse centrada em (r, –2r) com semi-eixos valendo r e 2r.
c) uma parábola com vértice em (r, –r).
d) duas retas paralelas distando r 3 uma da outra.
e) uma hipérbole centrada em (r, –2r) com semi-eixos valendo r.
Questão 08. U.Católica-DF – Durante uma guerrilha, os rebeldes dispararam um míssil visando atingir a sede do governo. O míssil descreveu uma parábola, que é o gráfico da função y = –x2 + 20x, com x e y em metros. Os soldados governistas dispararam um míssil para interceptar o primeiro, cuja trajetória é dada pela lei y = –x2 + 40x – 300.
Os mísseis irão se encontrar à altura de:
a) 30 m em relação ao solo.
b) 20 m em relação ao solo.
c) 15 m em relação ao solo.
d) 75 m em relação ao solo.
e) 50 m em relação ao solo.
Questão 09. PUC-SP – Um veículo foi submetido a um teste para a verificação do consumo de combustível. O teste consistia em fazer o veículo percorrer, várias vezes, em velocidade constante, uma distância de 100 km em estrada plana, cada vez a uma velocidade diferente. Observou-se então que, para velocidades entre 20 km/h e 120 km/h, o consumo de gasolina, em litros, era função da velocidade, conforme mostra o gráfico seguinte.
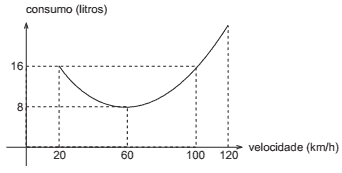
Se esse gráfico é parte de uma parábola, quantos litros de combustível esse veículo deve ter consumido no teste feito à velocidade de 120 km/h?
a) 20
b) 22
c) 24
d) 26
e) 28
Questão 10 sobre Parábola, Hipérbole e Elipse: UFMS – Em um laboratório, três tipos de bactérias, tipo A, tipo B e tipo C, estão sendo pesquisadas. Para uma das experiências, foram preparadas três lâminas, que ficaram em observação por um período de 3 dias. Em cada lâmina, no mesmo instante, foram colocadas culturas dos três tipos de bactéria, de acordo com o seguinte quadro:
lâmina 1 : cultura de bactérias do tipo A
lâmina 2 : cultura de bactérias do tipo B
lâmina 3 : cultura de bactérias do tipo C
Sabe-se que o número de bactérias em cada lâmina, em função do tempo t, em horas, durante o período da experiência é dado pelas funções definidas por:
bactérias do tipo A: a(t) = –10 t2 + 800t + 2000;
bactérias do tipo B: b(t) = –10t2 + 900t + 100;
bactérias do tipo C: c(t) = 50(mt + 60), onde m é um número real fixo.
Então, é correto afirmar que:
(01) Foram colocadas 900 bactérias do tipo B na lâmina 2.
(02) Desconhecendo o valor do número real m, não é possível determinar o número de bactérias do tipo C que foram colocadas na lâmina 3.
(04) Antes de completar 24 horas de experiência, a cultura da lâmina 1 e a cultura da lâmina 2 apresentaram, num mesmo instante, o mesmo número de bactérias.
(08) A população máxima da cultura da lâmina 1 foi de 16 000 bactérias.
(16) Se o valor de m é negativo, então a cultura da lâmina 3 sempre teve uma população menor do que a inicial.
Dê, como resposta, a soma das alternativas corretas.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos melhores sobre Parábola, Hipérbole e Elipse:
01. C;
02. C;
03. D;
04. C;
05. A;
06. A;
07. E;
08. D;
09. D;
10. 04 + 16 = 20
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
