Questão 01 sobre Poliedros, Esferas, Troncos e Sólidos: AEU-DF – Um prisma é um poliedro convexo que apresenta duas faces congruentes, dispostas em planos paralelos. Tais faces são chamadas bases do prisma. As demais faces de tal poliedro são paralelogramos que apresentam arestas comuns com as bases. De um certo prisma regular sabe-se que 12 de suas arestas medem 6 cm cada e suas outras 6 arestas têm medidas iguais a 20 cm.
Em relação a tal prisma analise e julgue os itens seguintes.
( ) As arestas que medem 20 cm podem ser as arestas das bases do prisma.
( ) O prisma é triangular, ou seja, sua base é um triângulo.
( ) Cada face lateral do prisma é um retângulo cuja área vale 120 cm2.
( ) A área da base do prisma corresponde à área de seis triângulos equiláteros de lado 6 cm.
( ) O volume do prisma é igual a 20.Ab, onde Ab é a medida da área de sua base.
Questão 02. Unifor-CE – Reduzindo-se a medida do raio de uma esfera em 20% de seu valor, o volume será reduzido em:
a) 48,8%
b) 51,2%
c) 54,6%
d) 56,4%
e) 62,8%
Questão 03. PUC-PR – Um poliedro convexo tem 7 faces. De um dos seus vértices partem 6 arestas e de cada um dos vértices restantes partem 3 arestas. Quantas arestas tem esse poliedro?
a) 8
b) 10
c) 12
d) 14
e) 16
Questão 04 sobre Poliedros, Esferas, Troncos e Sólidos: UEPI – Qual é o poliedro regular que tem 20 vértices e 30 arestas?
a) Hexaedro;
b) Octaedro;
c) Dodecaedro;
d) Icosaedro;
e) Tridecaedro.
Questão 05. I.E.Superior de Brasília-DF – O poliedro da figura ao abaixo é obtido a partir da secção de um cubo por planos perpendiculares às suas diagonais. Considere que cada plano secciona as três arestas que convergem em um dos vértices a um quarto de seu comprimento. O comprimento de cada aresta do cubo é de 12 cm.
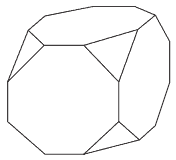
Analise e julgue os itens seguintes.
( ) O poliedro tem faces triangulares que são triângulos equiláteros.
( ) Cada um dos triângulos que são faces do poliedro tem área maior do que 5 cm2.
( ) O poliedro tem 14 faces e 24 vértices.
( ) A área total do poliedro apresentado na figura é igual à área total do cubo que o gerou.
( ) O volume do poliedro da figura é menor do que 1 700 cm3.
Questão 06. PUC-RS – Um poliedro convexo tem cinco faces triangulares e três pentagonais. O número de arestas e o número de vértices deste poliedro são, respectivamente:
a) 30 e 40
b) 30 e 24
c) 30 e 8
d) 15 e 25
e) 15 e 9
Questão 07 sobre Poliedros, Esferas, Troncos e Sólidos: U. Passo Fundo-RS – Dadas as afirmativas:
I. Um cubo de aresta de 3 cm tem área total igual a 54 cm2.
II. Uma pirâmide quadrangular regular com 3 cm de aresta da base e 5 cm de altura tem volume igual 18 cm3.
III. Um poliedro convexo de 3 faces triangulares e 3 faces pentagonais tem 8 vértices.
É verdadeiro o que se afirma em:
a) I apenas.
b) I e III apenas.
c) II e III apenas.
d) I e II apenas.
e) I, II e III.
Questão 08. UFCE – Um poliedro convexo de nove vértices possui quatro ângulos triédricos e cinco ângulos tetraédricos. Então o número de faces deste poliedro é:
a) 12
b) 11
c) 10
d) 9
e) 8
Questão 09. Fempar – Uma bola de sorvete tem 6 cm de diâmetro. Ao ingerir 20 bolas de sorvete, uma pessoa consumirá, em litros, aproximadamente:
(Obs.: Considerar que:
1) a bola de sorvete é perfeitamente esférica.
2) π = 3,14
3) o volume fundido é 50% menor que o volume da bola do sorvete)
a) 9,04
b) 0,904
c) 3,4
d) 1,13
e) 0,0113
Questão 10 sobre Poliedros, Esferas, Troncos e Sólidos: U. E. Ponta Grossa-PR – A relação entre o volume e a área de uma esfera é 1. Então, é correto afirmar que:
01) a área dessa esfera é igual a três vezes a área de uma esfera de 1 u.c. de raio.
02) o raio dessa esfera vale 3 u.c.
04) a aresta de um cubo circunscrito a essa esfera vale 6 u.c.
08) essa esfera pode ser inscrita num cilindro equilátero de altura 6 u.c.
16) a geratriz de um cone cujo raio da base tem a mesma medida do raio dessa esfera e cuja altura é 4 u.c. vale 5 u.c.
Dê, como resposta, a soma das alternativas corretas.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos melhores exercícios de Matemática sobre Poliedros, Esferas, Troncos e Sólidos:
01. F-F-V-V-V;
02. A;
03. C;
04. C;
04. V-V-V-F-V;
05. E;
07. B;
08. D;
09. D;
10. 30 = 02 + 04 + 08 + 16
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
