Questão 01. (UNIRIO-RJ) Sistemas Lineares Exercícios: Num determinado teste psicológico, existem 20 questões, com três opções de resposta a, b e c. Cada opção a vale +1, cada opção b vale 0, e cada opção c vale –1. Uma pessoa faz o teste, respondendo a todas as questões, com uma só resposta por questão, totalizando –5 pontos. Com as mesmas marcações, essa mesma pessoa totalizaria 54 pontos se cada opção a valesse +1, se cada opção b valesse +2, e se cada opção c valesse +4 pontos.
O número de marcações feitas por essa pessoa na opção b foi de:
A) 2
B) 4
C) 6
D) 7
E) 9
Questão 02. (UFU-MG) Considere o sistema linear S = , em que a é uma constante real. Sabendo-se que existe uma única reta r de coeficiente angular positivo, tal que todos os pares ordenados (x, y), que são soluções de S, satisfazem a equação de r, pode-se afirmar que:
A) necessariamente a é um número positivo.
B) existem exatamente dois valores possíveis para a nas condições do enunciado.
C) existe apenas um valor possível para a nas condições do enunciado.
D) a é divisível por 9.
Questão 03. (PUC Minas–2006) Para atender uma encomenda de fantasias, certa costureira comprou 3 m do tecido A e 2 m do tecido B, pagando R$ 25,50; depois, pagou R$ 46,50 na compra de 5 m do tecido A e 4 m do tecido B.
Finalmente, para retocar a costura, comprou mais 1 m de cada um desses tecidos. Sabendo-se que, pela mão de obra, essa costureira cobrou a mesma quantia gasta na compra dos tecidos, pode-se afirmar que o valor a ser pago pela encomenda, em reais, foi:
A) 144,00
B) 151,00
C) 165,00
D) 172,00
Questão 04. (UFV-MG–2007) Sistemas Lineares Exercícios: Um pecuarista fica sabendo que seus animais devem ingerir diariamente 60 g do nutriente A e 40 g do nutriente B.
Esse pecuarista dispõe de três tipos de ração, com as seguintes características, por quilograma:
I) A ração I contém 5 gramas do nutriente A e 8 gramas do nutriente B; custa R$ 4,00.
II) A ração II contém 5 gramas do nutriente A e 4 gramas do nutriente B; custa R$ 3,00.
III)A ração III contém 15 gramas do nutriente A e 8 gramas do nutriente B; custa R$ 8,00.
O pecuarista pretende misturar as rações І, II e III, de maneira que seus animais possam ingerir a quantidade de nutrientes recomendada. Se, além disso, ele deseja gastar exatamente R$ 32,00, é CORRETO afirmar que:
A) é impossível o pecuarista fazer a mistura de modo que seus animais possam ingerir diariamente 60 g do nutriente A, 40 g do nutriente B e gastar exatamente R$ 32,00.
B) é possível o pecuarista fazer a mistura combinando 2 kg da ração I, 4 kg da ração II e 2 kg da ração III.
C) a mistura deve ser feita combinando 1 kg da ração I, 4 kg da ração II e 2 kg da ração III.
D) existem várias formas de fazer a mistura de modo que seus animais possam ingerir diariamente 60 g do nutriente A, 40 g do nutriente B e gastar exatamente R$ 32,00.
E) a mistura deve ser feita combinando 4 kg da ração I, 4 kg da ração II e 2 kg da ração III.
Questão 05. (PUC-SP–2006) Uma pessoa tem 32 moedas, sendo x de 5 centavos, y de 10 centavos e z de 25 centavos, totalizando a quantia de R$ 4,95. Considerando os possíveis valores de x, y e z que satisfazem as condições dadas, qual das sentenças seguintes NUNCA poderia ser verdadeira?
A) x + y = 20
B) x + z = 25
C) x + z = 17
D) y + z = 25
E) y + z = 20
Questão 06. (UFRGS) Em cada prova de uma competição esportiva, foram distribuídas uma medalha de ouro (3 pontos), uma de prata (2 pontos) e uma de bronze (1 ponto). Foram realizadas dez provas, e três equipes conquistaram todas as medalhas da competição, sendo vencedora a equipe que obteve o maior número de pontos. Observe a tabela a seguir, que apresenta a distribuição das medalhas.
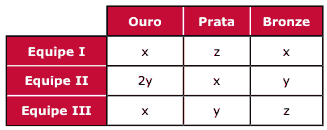
Considerando-se que a equipe III obteve 18 pontos, a equipe vencedora obteve:
A) 19 pontos.
B) 20 pontos.
C) 21 pontos.
D) 22 pontos.
E) 23 pontos.
Questão 07. (UFU-MG) Sistemas Lineares Exercícios: Somando-se as mesadas de Huguinho, Luizinho e Zezinho chega-se a um total de 45 reais. Dobrando-se a mesada de Huguinho e mantendo-se os valores das outras duas, o total passa a ser de 55 reais; e dobrando-se as mesadas de Huguinho e de Luizinho e mantendo-se o valor da mesada de Zezinho, o total passa a ser de 70 reais.
Multiplicando-se os valores numéricos das três mesadas obtemos:
A) 4 500
B) 2 000
C) 1 500
D) 3 000
Questão 08. (PUC-SP) Sabe-se que, na compra de uma caixa de lenços, dois bonés e três camisetas, gasta-se um total de R$ 127,00. Se três caixas de lenços, quatro bonés e cinco camisetas, dos mesmos tipos que os primeiros, custam juntos R$ 241,00, a quantia a ser desembolsada na compra de apenas três unidades desses artigos, sendo um de cada tipo, será:
A) R$ 72,00.
B) R$ 65,00.
C) R$ 60,00.
D) R$ 57,00.
E) R$ 49,00.
Questão 09. (ENEM) Um investidor montou uma carteira de aplicação em dois ativos A e B na bolsa de valores. Sabe-se que ele aplicou R$ 30 000,00 nessa carteira. Passados seis meses, o investidor verificou que o ativo A sofreu uma desvalorização de 40%, enquanto o ativo B sofreu uma valorização de 20%.
Com isso, seu saldo total tornou-se igual a R$ 25 200,00. Pode se afirmar que:
A) o total aplicado no ativo A foi 30% maior do que o total aplicado no ativo B.
B) o valor aplicado no ativo B representa 40% do total aplicado pelo investidor.
C) o prejuízo total do investidor representa 20% do total aplicado no ativo A.
D) a diferença entre os valores aplicados nos ativos A e B é igual a R$ 4 000,00.
E) após a desvalorização, o saldo da aplicação no ativo A tornou-se igual a R$ 12 000,00.
Questão 10. (Enem–2000) Sistemas Lineares Exercícios: Uma companhia de seguros levantou dados sobre os carros de determinada cidade e constatou que são roubados, em média, 150 carros por ano. O número de carros roubados da marca X é o dobro do número de carros roubados da marca Y, e as marcas X e Y juntas respondem por cerca de 60% dos carros roubados.
O número esperado de carros roubados da marca Y é:
A) 20
B) 30
C) 40
D) 50
E) 60
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da melhor lista de exercícios de Matemática sobre Sistemas Lineares Exercícios:
01. D;
02. C;
03. C;
04. A;
05. E;
06. D;
07. D;
08. D;
09. B;
10. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
