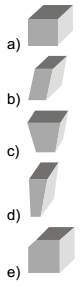
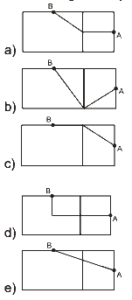
Questão 01 sobre Geometria Espacial: (Enem 2ª aplicação 2010) Para confeccionar, em madeira, um cesto de lixo que comporá o ambiente decorativo de uma sala de aula, um marceneiro utilizará, para as faces laterais, retângulos e trapézios isósceles e, para o fundo, um quadrilátero, com os lados de mesma medida e ângulos retos. Qual das figuras representa o formato de um cesto que possui as características estabelecidas?
Questão 02. (Enem 2010) Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura.
Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a
a) 5 cm.
b) 6 cm.
c) 12 cm.
d) 24 cm.
e) 25 cm.
Questão 03. (Enem 2010) A siderúrgica “Metal Nobre” produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralepípedo retangular, de acordo com as dimensões indicadas na figura que segue.
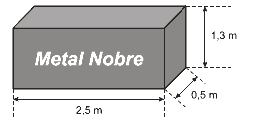
O produto das três dimensões indicadas na peça resultaria na medida da grandeza
a) massa.
b) volume.
c) superfície.
d) capacidade.
e) comprimento.
Questão 04 sobre Geometria Espacial: (Enem 2010) Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro e vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que e interno, mede 8 cm.
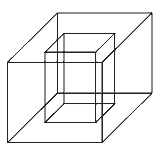
O volume de madeira utilizado na confecção desse objeto foi de
a) 12 cm3.
b) 64 cm3.
c) 96 cm3.
d) 1 216 cm3.
e) 1 728 cm3.
Questão 05. (Enem 2ª aplicação 2010) A figura seguinte ilustra um salão de um clube onde estão destacados os pontos A e B.
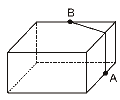
Nesse salão, o ponto em que chega o sinal da TV a cabo fica situado em A. A fim de instalar um telão para a transmissão dos jogos de futebol da Copa do Mundo, esse sinal deverá ser levado até o ponto B por meio de um cabeamento que seguirá na parte interna da parede e do teto. O menor comprimento que esse cabo deverá ter para ligar os pontos A e B poderá ser obtido por meio da seguinte representação no plano:
Questão 06. (Enem 2ª aplicação 2010) Devido aos fortes ventos, uma empresa exploradora de petróleo resolveu reforçar a segurança de suas plataformas marítimas, colocando cabos de aço para melhor afixar a torre central. Considere que os cabos ficarão perfeitamente esticados e terão uma extremidade no ponto médio das arestas laterais da torre central (pirâmide quadrangular regular) e a outra no vértice da base da plataforma (que é um quadrado de lados paralelos aos lados da base da torre central e centro coincidente com o centro da base da pirâmide), como sugere a ilustração.
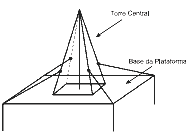
Se a altura e a aresta da base da torre central medem, respectivamente, 24 m e 6 √2m e o lado da base da plataforma mede 19 √2m, então a medida, em metros, de cada cabo será igual a:
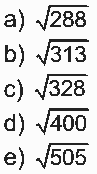
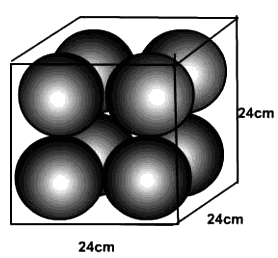
Questão 07 sobre Geometria Espacial: (Enem 2009) Uma empresa que fabrica esferas de aço, de 6 cm de raio, utiliza caixas de madeira, na forma de um cubo, para transportá-las. Sabendo que a capacidade da caixa é de 13.824 cm3, então o número máximo de esferas que podem ser transportadas em uma caixa é igual a
a) 4.
b) 8.
c) 16.
d) 24.
e) 32.
Questão 08. (Enem cancelado 2009) Considere um caminhão que tenha uma carroceria na forma de um paralelepípedo retângulo, cujas dimensões internas são 5,1 m de comprimento, 2,1 m de largura e 2,1 m de altura. Suponha que esse caminhão foi contratado para transportar 240 caixas na forma de cubo com 1 m de aresta cada uma e que essas caixas podem ser empilhadas para o transporte.
Qual é o número mínimo de viagens necessárias para realizar esse transporte?
a) 10 viagens.
b) 11 viagens.
c) 12 viagens.
d) 24 viagens.
e) 27 viagens.
Questão 09. (Enem simulado 2009) Com o objetivo de trabalhar com seus alunos o conceito de volume de sólidos, um professor fez o seguinte experimento: pegou uma caixa de polietileno, na forma de um cubo com 1 metro de lado, e colocou nela 600 litros de água. Em seguida, colocou, dentro da caixa com água, um sólido que ficou completamente submerso. Considerando que, ao colocar o sólido dentro da caixa, a altura do nível da água passou a ser 80 cm, qual era o volume do sólido?
a) 0,2 m3
b) 0,48 m3
c) 4,8 m3
d) 20 m3
e) 48 m3
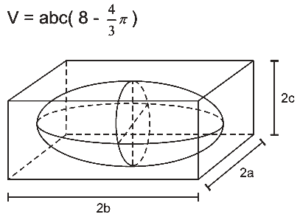
Questão 10 sobre Geometria Espacial: (Enem simulado 2009) Uma elipse é uma seção plana de um cilindro circular reto, em que o plano que intersecta o cilindro é oblíquo ao eixo do cilindro (Figura 1). É possível construir um sólido de nome elipsoide que, quando seccionado por três planos perpendiculares entre si, mostram elipses de diferentes semieixos a, b e c, como na Figura 2. O volume de um elipsoide de semieixos a, b e c é dado por ![]() .
.
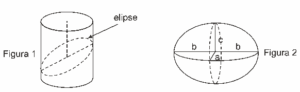
Considere que um agricultor produz melancias, cujo formato é aproximadamente um elipsoide, e ele deseja embalar e exportar suas melancias em caixas na forma de um paralelepípedo retângulo. Para melhor acondicioná-las, o agricultor preencherá o espaço vazio da caixa com material amortecedor de impactos (palha de arroz/serragem/bolinhas de isopor). Suponha que sejam a, b e c, em cm, as medidas dos semieixos do elipsoide que modela as melancias, e que sejam 2a, 2b e 2c, respectivamente, as medidas das arestas da caixa. Nessas condições, qual é o volume de material amortecedor necessário em cada caixa?
a) V = 8abc cm3
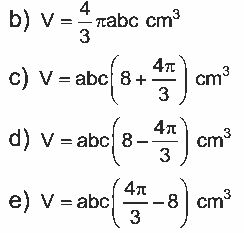
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos 10 exercícios de matemática sobre Geometria Espacial:
01. C
A única figura que representa um cesto com apenas trapézios isósceles e retângulos nas faces laterais é a da alternativa (C).
02. B
Sendo a a aresta do cubo, temos:
a3 = 4.18.3
a3 = 216
a = 6
03. B
Multiplicando as dimensões temos o valor de seu volume em m3.
04. D
V = volume do cubo maior – volume do cubo menor
V = 123 – 83
V = 1728 – 512
V = 1216
05. E
Sabendo que a menor distância entre dois pontos é o segmento de reta que os une, segue que a representação exibida na alternativa (E) é a única que ilustra corretamente a menor distância entre A e B.
06. D
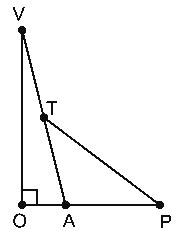
Considere a figura abaixo, em que o quadrado ABCD é a base da pirâmide, O é o centro da base da pirâmide e o quadrado PQRS é a base da plataforma.
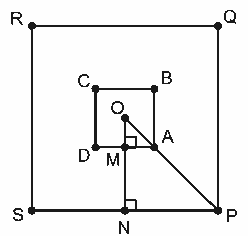
Como ![]() . Além disso, sabemos que
. Além disso, sabemos que ![]() Logo,
Logo, 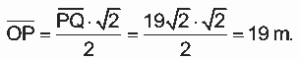

Aplicando o Teorema de Pitágoras no triângulo VOA, obtemos:
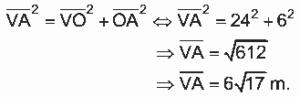
Queremos calcular PT, em que T é o ponto médio da aresta lateral da torre, conforme a figura seguinte.
Aplicando a Lei dos Cossenos no triângulo APT, segue que ![]()
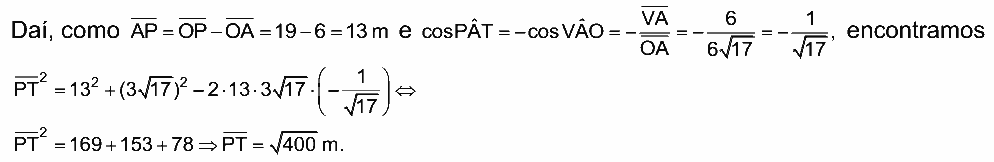
07. B
a3 = 13.824 <-> a = 24cm. Diâmetro da esfera = 12cm No comprimento do cubo podemos colocar 2 esferas Na largura do cubo podemos colocar 2 esferas Na altura do cubo podemos colocar 2 esferas Logo o número de esferas será 2.2.2 = 8
08. C
No comprimento conseguiremos colocar 5 caixas, na largura 2 caixas e na altura 2 caixas. Total de caixas 5.2.2 = 20 caixas. Número mínimo de viagens: 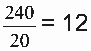
09. A
Cálculo da altura inicial do líquido. 1.1.x = 0,6 m3 <-> x = 0,6 m <-> x = 60 cm
O volume do sólido será igual ao volume de água deslocado. V = 1.1.(0,8 – 0,6) = 0,2 m3
10.D
V = V(caixa) – V (melancia)
V = 2a.2b.2c – ![]()
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína

A resposta correta ao exercício (6) é “b”, e não “d”, ou seja, o cabo tem tamanho = raiz(313).
Se o cabo bate no meio da aresta lateral, a altura da ponta mais alta do cabo (por semelhança de triângulos) é 12m (metade da altura da torre). Daí, (cabo)2 = (12)2 + (distância f)2.
Distância f é a distância entre P e metade da distância OA (também por semelhança de triângulos, o cabo encontra com a lateral da torre exatamente na metade da distância OA, se projetássemos o cabo na plataforma).
Para calcular f, chamarei de b = PN-(AM/2), ou seja, b = {[19.raiz(2)]-[6.raiz(2)]}/2 = 13.raiz(2)/2.
Daí f2 = b2 + b2 = 2 . b2 = 2 . 169.2/4 = 169 então f=raiz(169) = 13
Então o cabo é dado pela equação:
(cabo)2 = (12)2 + (13)2 = 144+169 = 313
Então:
cabo = raiz(313)