Questão 01. (Enem 2011) Simulado sobre Geometria Espacial: A figura seguinte mostra um modelo de sombrinha muito usado em países orientais.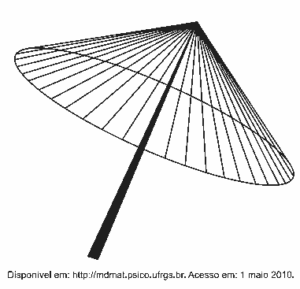
Esta figura é uma representação de uma superfície de revolução chamada de
a) pirâmide.
b) semiesfera.
c) cilindro.
d) tronco de cone.
e) cone.
Questão 02. (Enem 2ª aplicação 2010) Um fabricante de creme de leite comercializa seu produto em embalagens cilíndricas de diâmetro da base medindo 4 cm e altura 13,5 cm. O rótulo de cada uma custa R$ 0,60. Esse fabricante comercializará o referido produto em embalagens ainda cilíndricas de mesma capacidade, mas com a medida do diâmetro da base igual à da altura. Levando-se em consideração exclusivamente o gasto com o rótulo, o valor que o fabricante deverá pagar por esse rótulo é de:
a) R$ 0,20, pois haverá uma redução de ![]() na superfície da embalagem coberta pelo rótulo.
na superfície da embalagem coberta pelo rótulo.
b) R$ 0,40, pois haverá uma redução de ![]() na superfície da embalagem coberta pelo rótulo.
na superfície da embalagem coberta pelo rótulo.
c) R$ 0,60, pois não haverá alteração na capacidade da embalagem.
d) R$ 0,80, pois haverá um aumento de ![]() na superfície da embalagem coberta pelo rótulo.
na superfície da embalagem coberta pelo rótulo.
e) R$ 1,00, pois haverá um aumento de ![]() na superfície da embalagem coberta pelo rótulo.
na superfície da embalagem coberta pelo rótulo.
Questão 03. (Enem 2010) Simulado sobre Geometria Espacial: Alguns testes de preferência por bebedouros de água foram realizados com bovinos, envolvendo três tipos de bebedouros, de formatos e tamanhos diferentes. Os bebedouros 1 e 2 têm a forma de um tronco de cone circular reto, de altura igual a 60 cm, e diâmetro da base superior igual a 120 cm e 60 cm, respectivamente. O bebedouro 3 é um semicilindro, com 30 cm de altura, 100 cm de comprimento e 60 cm de largura. Os três recipientes estão ilustrados na figura.
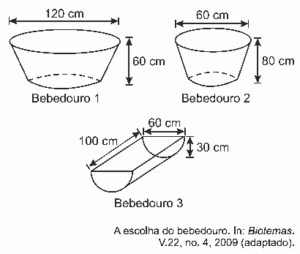
Considerando que nenhum dos recipientes tenha tampa, qual das figuras a seguir representa uma planificação para o bebedouro 3?
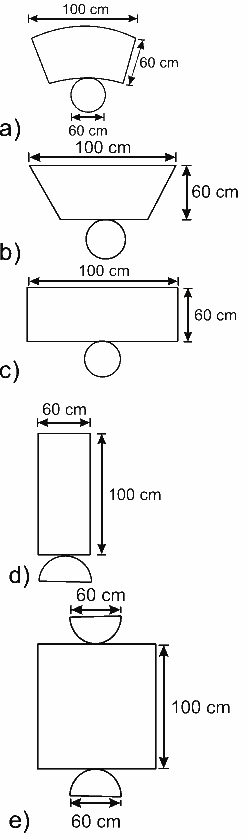
Questão 04. (Enem 2ª aplicação 2010) Simulado sobre Geometria Espacial: Uma fábrica de tubos acondiciona tubos cilíndricos menores dentro de outros tubos cilíndricos. A figura mostra uma situação em que quatro tubos cilíndricos estão acondicionados perfeitamente em um tubo com raio maior
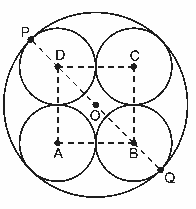
Suponha que você seja o operador da máquina que produzirá os tubos maiores em que serão colocados, sem ajustes ou folgas, quatro tubos cilíndricos internos. Se o raio da base de cada um dos cilindros menores for igual a 6 cm, a máquina por você operada deverá ser ajustada para produzir tubos maiores, com raio da base igual a:
a) 12 cm
b) 12 √2cm
c) 24 √2cm
d) 6 (1 + √2) cm
e) 12 (1 + √2) cm
Questão 05. (Enem 2ª aplicação 2010) João tem uma loja onde fabrica e vende moedas de chocolate com diâmetro de 4 cm e preço de R$ 1,50 a unidade. Pedro vai a essa loja e, após comer várias moedas de chocolate, sugere ao João que ele faça moedas com 8 cm de diâmetro e mesma espessura e cobre R$ 3,00 a unidade.
Considerando que o preço da moeda depende apenas da quantidade de chocolate, João:
a) aceita a proposta de Pedro, pois, se dobra o diâmetro, o preço também deve dobrar.
b) rejeita a proposta de Pedro, pois o preço correto seria R$ 12,00.
c) rejeita a proposta de Pedro, pois o preço correto seria R$ 7,50.
d) rejeita a proposta de Pedro, pois o preço correto seria R$ 6,00.
e) rejeita a proposta de Pedro, pois o preço correto seria R$ 4,50.
Questão 06. (Enem 2010) Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
a) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
b) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
c) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
d) encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
e) encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
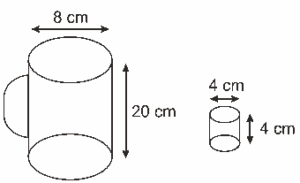
Questão 07. (Enem 2ª aplicação 2010) Simulado sobre Geometria Espacial: Certa marca de suco é vendida no mercado em embalagens tradicionais de forma cilíndrica. Relançando a marca, o fabricante pôs à venda embalagens menores, reduzindo a embalagem tradicional à terça parte de sua capacidade. Por questões operacionais, a fábrica que fornece as embalagens manteve a mesma forma, porém reduziu à metade o valor do raio da base da embalagem tradicional na construção da nova embalagem. Para atender à solicitação de redução da capacidade, após a redução no raio, foi necessário determinar a altura da nova embalagem.
Que expressão relaciona a medida da altura da nova embalagem de suco (a) com a altura da embalagem tradicional (h)?
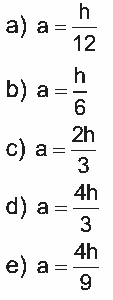
Questão 08. (Enem 2ª aplicação 2010) Uma empresa de refrigerantes, que funciona sem interrupções, produz um volume constante de 1 800 000 cm3 de líquido por dia. A máquina de encher garrafas apresentou um defeito durante 24 horas. O inspetor de produção percebeu que o líquido chegou apenas à altura de 12 cm dos 20 cm previstos em cada garrafa. A parte inferior da garrafa em que foi depositado o líquido tem forma cilíndrica com raio da base de 3 cm. Por questões de higiene, o líquido já engarrafado não será reutilizado.
Utilizando π ≅ 3, no período em que a máquina apresentou defeito, aproximadamente quantas garrafas foram utilizadas?
a) 555
b) 5555
c) 1333
d) 13333
e) 133333
Questão 09. (Enem 2010) Para construir uma manilha de esgoto, um cilindro com 2 m de diâmetro e 4 m de altura (de espessura desprezível), foi envolvido homogeneamente por uma camada de concreto, contendo 20 cm de espessura.
Supondo que cada metro cúbico de concreto custe R$ 10,00 e tomando 3,1 como valor aproximado de π, então o preço dessa manilha é igual a
a) R$ 230,40.
b) R$ 124,00.
c) R$104,16.
d) R$ 54,56.
e) R$ 49,60.
Questão 10. (Enem 2010) Simulado sobre Geometria Espacial: No manejo sustentável de florestas, é preciso muitas vezes obter o volume da tora que pode ser obtida a partir de uma árvore. Para isso, existe um método prático, em que se mede a circunferência da árvore à altura do peito de um homem (1,30 m), conforme indicado na figura. A essa medida denomina-se “rodo” da árvore. O quadro a seguir indica a fórmula para se cubar, ou seja, obter o volume da tora em m3 a partir da medida do rodo e da altura da árvore.

Um técnico em manejo florestal recebeu a missão de cubar, abater e transportar cinco toras de madeira, de duas espécies diferentes, sendo:
• 3 toras da espécie I, com 3 m de rodo, 12 m de comprimento e densidade 0,77 toneladas/m3;
• 2 toras da espécie II, com 4 m de rodo, 10 m de comprimento e densidade 0,78 toneladas/m3.
Após realizar seus cálculos, o técnico solicitou que enviassem caminhões para transportar uma carga de, aproximadamente,
a) 29,9 toneladas.
b) 31,1 toneladas.
c) 32,4 toneladas.
d) 35,3 toneladas.
e) 41,8 toneladas.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas do melhor Simulado sobre Geometria Espacial para passar no Enem e Vestibular:
01. E
A expressão superfície de revolução garante que a figura represente a superfície lateral de um cone.
02. B
Sejam r1 = 2cm e h1 = 13,5cm, respectivamente, o raio da base e a altura do cilindro cujo rótulo custa
R$ 0,60.
Se V1 e Al 1 denotam, respectivamente, a capacidade e a área do rótulo, então
V1 = π2.22 .13,5 = 54cm3 1 e Al1 = 2. π.2.13,5 = 54πcm2
Sejam r2 e h2 , respectivamente, o raio da base e a altura da nova embalagem. Como h2 =2.r2 e
as capacidades das embalagens são iguais, temos que ![]() Além disso, a área lateral da nova embalagem é Al2 = 2.π.3.6=36πcm2.
Além disso, a área lateral da nova embalagem é Al2 = 2.π.3.6=36πcm2.
Supondo que o custo da embalagem seja diretamente proporcional à área lateral da mesma, obtemos 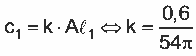 sendo k a constante de proporcionalidade e c1 o custo da primeira
sendo k a constante de proporcionalidade e c1 o custo da primeira
embalagem. Portanto, ![]() ou seja, o valor que o fabricante deverá pagar por esse rótulo é de R$ 0,40, pois haverá uma redução de
ou seja, o valor que o fabricante deverá pagar por esse rótulo é de R$ 0,40, pois haverá uma redução de 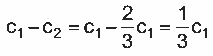 na superfície da embalagem coberta pelo rótulo.
na superfície da embalagem coberta pelo rótulo.
03. E
A superfície do bebedouro 3 é constituída por dois semicírculos e por um retângulo.
04. D
Considere a figura, em que O é o centro da base do cilindro cujo raio queremos calcular.

O lado do quadrado ABCD é igual ao diâmetro da base dos cilindros menores. Logo, ![]() 2.6=12cm. Além disso, como
2.6=12cm. Além disso, como 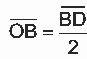 , segue que
, segue que 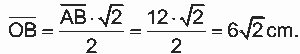 Portanto, o raio da base do cilindro maior é dado por
Portanto, o raio da base do cilindro maior é dado por ![]()
05. D
Sejam r e h, respectivamente, o raio e a espessura das moedas de chocolate fabricadas atualmente. Logo, o volume V de chocolate de uma moeda é V = π.r2 .h. De acordo com a sugestão de Pedro, o volume V’ de chocolate empregado na fabricação de uma moeda com 8cm de diâmetro seria ![]()
Supondo que o preço p da moeda seja diretamente proporcional ao volume de chocolate, segue que p = k.V = R$1,50, em que k é a constante de proporcionalidade. Assim, o preço p’ da moeda sugerida por Pedro deveria ser de p’ = k.V’ = k.4V = 4.1,50 = R$ 6,00.
06. A
Volume do copinho = π.22 .4 = 16π cm3
Volume de 20 copinhos pela metade = ½20.16π cm2 = 160π cm3
Volume da leiteira = π.42.20 = 320π cm3
07. D
Sejam v e v ‘, respectivamente, a capacidade da embalagem tradicional e a capacidade da nova embalagem. Portanto, de acordo com o enunciado, temos 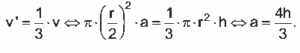
08. B
O volume de refrigerante em uma garrafa parcialmente cheia é dado por π.32 .12≅3.9.12=324cm3 . Portanto, o número aproximado de garrafas utilizadas foi de 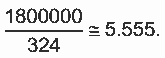
09. D
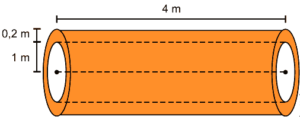
Volume do concreto é V. Logo:
V = Volume do cilindro maior – volume do cilindro menor
V = π.(1,2)2 .4 – π.12.4
V = 1,76.3,1
V= 5,456m3
Logo, o preço da manilha será 5,456 . 10 = R$ 54,56
10.A
| Volume ( m3 ) | Massa (toneladas) | |
| Espécie I | 3.32.12.0,06=19,44 | 0,77.19,44 = 14,96 |
| Espécie II | 2.42.10.0,06 = 19,2 | 0,78.19,2 = 14,97 |
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
