10 Atividades sobre Geometria Espacial de Posição e Poliedros

Questão 01 sobre Geometria Espacial de Posição e Poliedros: (Espcex) Considere a seguintes proposições:

I. Toda reta paralela a um plano é paralela a qualquer reta desse plano.

II. Uma reta e um ponto determinam sempre um plano.

III. Se uma reta é perpendicular a duas retas concorrentes de um plano, então ela é perpendicular a esse plano.

Pode-se afirmar que:
a) só I é verdadeira.
b) só III é verdadeira.
c) só I e III são verdadeiras.
d) só III é falsa.
e) só I e III são falsas.

Questão 02. (Ufal) Se uma reta r é perpendicular a dois planos α e β, α ≠ β, então é verdade que:

a) a é paralelo a qualquer plano que contenha r.
b) b contém todas as retas perpendiculares a r.
c) a distância entre a e b é igual a 10 cm.
d) a e b são paralelos entre si.
e) a e b são perpendiculares entre si.

Questão 03. (Mackenzie) r, s, t são retas distintas tais que s é perpendicular a r e t é perpendicular a r. Relativamente às retas s e t, podemos afirmar que:

a) elas podem ser unicamente paralelas ou concorrentes.
b) elas podem ser unicamente paralelas ou reversas.
c) elas podem ser unicamente concorrentes ou reversas.
d) elas podem ser paralelas, concorrentes ou reversas.
e) elas podem ser unicamente reversas.

Questão 04 sobre Geometria Espacial de Posição e Poliedros: (Fuvest 2009) O ângulo q formado por dois planos α e β é tal que tgθ = . O ponto P pertence a a e a distância de P a b vale 1. Então, a distância de P à reta intersecção de a e b é igual a:

a) √3
b) √5
c) √6
d) √7
e)  √8

Questão 05. (UECE 2016) Um poliedro convexo com 32 vértices possui apenas faces triangulares. O número de arestas deste poliedro é

a) 100.
b) 120.
c) 90.
d) 80.

Questão 06. (UECE 2014) Um poliedro convexo tem 32 faces, sendo 20 hexágonos e 12 pentágonos. O número de vértices deste polígono:

a) 90.
b) 72.
c) 60.
d) 56.

Questão 07 sobre Geometria Espacial de Posição e Poliedros: (Cefet MG 2014) No contexto da Geometria Espacial, afirma-se:

I. Se uma reta é paralela a um plano, então ela está contida nesse plano.
II. Duas retas sem ponto comum são paralelas ou reversas.
III. Se dois planos são paralelos, então toda reta de um deles é paralela ao outro.
IV. Duas retas distintas paralelas a um plano são paralelas entre si.

São corretas apenas as afirmativas
a) I e II.
b) I e III.
c) II e III.
d) II e IV.
e) III e IV.

Questão 08. (CFTMG 2014) A figura a seguir representa uma cadeira onde o assento é um paralelogramo perpendicular ao encosto.

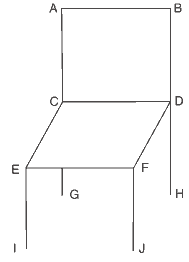
A partir dos pontos dados, é correto afirmar que os segmentos de retas
a) CD e EF são paralelos.
b) BD e FJ são concorrentes.
c) AC e CD são coincidentes.
d) AB e EI são perpendiculares.

Questão 09. (Fuvest 97) Uma formiga resolveu andar de um vértice a outro do prisma reto de bases triangulares ABC e DEG, seguindo um trajeto especial. Ela partiu do vértice G, percorreu toda a aresta perpendicular à base ABC, para em seguida caminhar toda a diagonal da face ADGC e, finalmente, completou seu passeio percorrendo a aresta reversa a CG. A formiga chegou ao vértice:

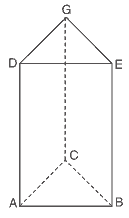
a) A
b) B
c) C
d) D
e) E

Questão 10 sobre Geometria Espacial de Posição e Poliedros: (UEM 2012) Sabendo que r, s e t são três retas no espaço tridimensional com r e s paralelas distintas, assinale o que for correto.

01) Se a reta r é perpendicular a um plano a, então a reta s também é perpendicular ao plano a.
02) Se a reta t é concorrente com a reta s, então t também é concorrente com a reta r.
04) Se um plano b contém a reta s, então o plano b também contém a reta r.
08) Se a reta t é perpendicular à reta r, então t é perpendicular ou ortogonal à reta s.
16) Se as três retas r, s e t são paralelas distintas, então existe um plano que contém as três retas.

🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.

Gabarito com as respostas das 10 atividades de matemática sobre Geometria Espacial de Posição e Poliedros:

01) b;

02) d;

03) d;

04) c;

05) c;

06) c;

07) c;

08) a;

09) e;

10) 01 + 08 = 09

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína