Questão 01 sobre Teorema de Tales e Quadriláteros: (UFMG) Sobre figuras planas, é CORRETO afirmar que:
A) um quadrilátero convexo é um retângulo, se os lados opostos têm comprimentos iguais.
B) um quadrilátero que tem suas diagonais perpendiculares é um quadrado.
C) um trapézio que tem dois ângulos consecutivos congruentes é isósceles.
D) um triângulo equilátero é também isósceles.
E) um triângulo retângulo é aquele cujos ângulos são retos.
Questão 02. (PUC Minas) Um trapézio isósceles, de 12 cm de altura, tem bases medindo 4 cm e 6 cm. Unindo-se os pontos médios de seus lados, obteremos um quadrilátero cujo perímetro mede:
A) 20 cm.
B) 24 cm.
C) 26 cm.
D) 30 cm.
Questão 03. (PUC-Campinas-SP–2007) Na figura a seguir, as retas r, s e t são paralelas entre si.
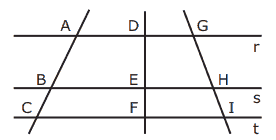
Se AC = x, BC = 8, DE = 15, EF = x – 10, GI = y e HI = 10, então x + y é um número:
A) maior que 47.
B) entre 41 e 46.
C) menor que 43.
D) quadrado perfeito.
E) cubo perfeito.
Questão 04 sobre Teorema de Tales e Quadriláteros: (UFV-MG–2007) Sob duas retas paralelas de uma cidade, serão construídos, a partir das estações A e B, passando pelas estações C e D, dois túneis retilíneos, que se encontrarão na estação X, conforme ilustra a figura a seguir:
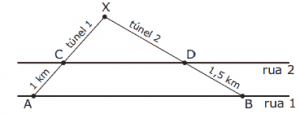
A distância entre as estações A e C é de 1 km e entre as estações B e D, de 1,5 km. Em cada um dos túneis, são perfurados 12 m por dia. Sabendo que o túnel 1 demandará 250 dias para ser construído e que os túneis deverão se encontrar em X, no mesmo dia, é CORRETO afirmar que o número de dias que a construção do túnel 2 deverá anteceder à do túnel 1 é:
A) 135
B) 145
C) 125
D) 105
E) 115
Questão 05. (PUC-Campinas-SP) Considere as afirmações:
I – Todo retângulo é um paralelogramo.
II – Todo quadrado é um retângulo.
III – Todo losango é um quadrado.
Associe a cada uma delas a letra v, se for VERDADEIRA, ou F, caso seja FALSA. Na ordem apresentada, temos:
A) F F F.
B) F F V.
C) V F F.
D) V V F.
E) N.d.a.
Questão 06. (UFV-MG) Em um trapézio isósceles de bases diferentes, uma diagonal é também bissetriz de um ângulo adjacente à base maior.
Isso significa que:
A) os ângulos adjacentes à base menor não são congruentes.
B) a base menor tem medida igual à dos lados oblíquos.
C) as diagonais se interceptam formando ângulo reto.
D) a base maior tem medida igual à dos lados oblíquos.
E) as duas diagonais se interceptam no seu ponto médio.
Questão 07 sobre Teorema de Tales e Quadriláteros: (FUVEST-SP) No retângulo a seguir, o valor, em graus, de a + b é:
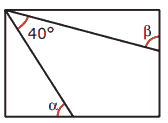
A) 50
B) 90
C) 120
D) 130
E) 220
Questão 08. (FUVEST-SP) Um trapézio retângulo tem bases 5 e 2 e altura 4. O perímetro desse trapézio é:
A) 13
B) 14
C) 15
D) 16
E) 17
Questão 09. (Enem–2000) Um marceneiro deseja construir uma escada trapezoidal com 5 degraus, de forma que o mais baixo e o mais alto tenham larguras, respectivamente, iguais a 60 cm e a 30 cm, conforme a figura.

Os degraus serão obtidos cortando-se uma peça linear de madeira cujo comprimento mínimo, em cm, deve ser:
A) 144
B) 180
C) 210
D) 225
E) 240
Questão 10 sobre Teorema de Tales e Quadriláteros: (Enem–2010) A loja Telas & Molduras cobra 20 reais por metro quadrado de tela, 15 reais por metro linear de moldura, mais uma taxa fixa de entrega de 10 reais. Uma artista plástica precisa encomendar telas e molduras a essa loja, sufi cientes para 8 quadros retangulares (25 cm x 50 cm).
Em seguida, fez uma segunda encomenda, mas agora para 8 quadros retangulares (50 cm x 100 cm). O valor da segunda encomenda será:
A) o dobro do valor da primeira encomenda, porque a altura e a largura dos quadros dobraram.
B) maior do que o valor da primeira encomenda, mas não o dobro.
C) a metade do valor da primeira encomenda, porque a altura e a largura dos quadros dobraram.
D) menor do que o valor da primeira encomenda, mas não a metade.
E) igual ao valor da primeira encomenda, porque o custo de entrega será o mesmo.

Gabarito com as respostas dos exercícios de Matemática sobre Teorema de Tales e Quadriláteros:
01. D;
02. C;
03. B;
04. C;
05. D;
06. B;
07. D;
08. D;
09. D;
10. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
