Questão 01 sobre Posições Relativas entre Retas: (Fuvest) As retas r e s são perpendiculares e interceptam-se no ponto (2, 4). A reta s passa pelo ponto (0, 5). Uma equação da reta r é:
a) 2y + x = 10
b) y = x + 2
c) 2y – x = 6
d) 2x + y = 8
e) y = 2x
Questão 02. (UEM) Considere as retas perpendiculares r e s de equações y = ax − 3 e y = 2x + b, respectivamente. Sabendo que a, 2 e b estão, nessa ordem, em uma progressão geométrica, é correto afirmar que o ponto de intersecção de r e s é:
a) (2, –4).
b) ( –3, 2).
c) ( –3, –4).
d) (2, –3).
e) (4, –2).
Questão 03. (UFSCar) Considere P um ponto pertencente à reta (r) de equação 3x + 5y – 10 = 0 e equidistante dos eixos coordenados. A equação da reta que passa por P e é perpendicular a (r) é:
a) 10x – 6y – 5 = 0
b) 6x – 10y + 5 = 0
c) 15x – 9y – 16 = 0
d) 5x + 3y – 10 = 0
e) 15x – 3y – 4 = 0
Questão 04 sobre Posições Relativas entre Retas: (Unemat) Dada a equação de reta (s): 2x – y + 1 = 0, a equação da reta paralela a s pelo ponto P(1, 1) será:
a) 2x – y = 0
b) 2x + y + 1 = 0
c) 2x + y – 1 = 0
d) 2x – y – 1 = 0
e) 2x – y + 2 = 0
Questão 05. (FGV 2001) A reta perpendicular à reta (r) 2x – y = 5, e passando pelo ponto P(1, 2), intercepta o eixo das abscissas no ponto:
a) (9/2, 0)
b) (5, 0)
c) (11/2, 0)
d) (6, 0)
e) (13/2, 0)
Questão 06. (Unifesp) Considere as retas:
(r) 5x – 12y = 42
(s) 5x + 16y = 56
(t) 5x + 20y = m
O valor de m para que as três retas sejam concorrentes num mesmo ponto é:
a) 14
b) 28
c) 36
d) 48
e) 58
Questão 07 sobre Posições Relativas entre Retas: (Fuvest) Os pontos M = (2 ; 2), N = (–4 ; 0) e P = (–2 ; 4) são, respectivamente, os pontos médios dos lados AB, BC e CA do triângulo ABC. A reta mediatriz do lado AB tem equação:
a) x + 2y – 6 = 0
b) x – 2y + 2 = 0
c) 2x – 2y – 2 = 0
d) 2x + y + 6 = 0
e) – x + 2y + 6 = 0
Questão 08. (UFPR 2011) Um balão de ar quente foi lançado de uma rampa inclinada. Utilizando o plano cartesiano, a figura abaixo descreve a situação de maneira simplificada.
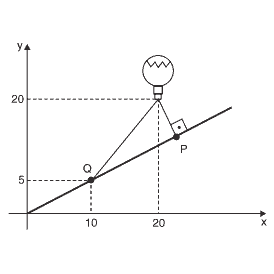
Ao ser lançado, o balão esticou uma corda presa aos pontos P e Q, mantendo-se fixo no ar. As coordenadas do ponto P, indicado na figura, são, então:
a) (21,7).
b) (22,8).
c) (24,12).
d) (25,13).
e) (26,15).
Questão 09. (FGV 2003) No plano cartesiano, os pontos A (- 1, 4) e B (3, 6) são simétricos em relação à reta (r). O coeficiente angular da reta (r) vale:
a) –1
b) –2
c) –3
d) –4
e) –5
Questão 10 sobre Posições Relativas entre Retas: (Uece) A reta que passa pelo ponto (2,1) e forma um ângulo de 45° com a reta 2x + 3y + 4 = 0 é dada pela equação:
a) 2x – y – 3 = 0
b) x – 3y + 1 = 0
c) 3x – y – 5 = 0
d) x – 5y + 3 = 0
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista com 10 exercícios de matemática para Enem sobre Posições Relativas entre Retas:
01) e;
02) a;
03) a;
04) d;
05) b;
06) e;
07) a;
08) c;
09) b;
10) d
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
