Questão 01 sobre Área e Volume do Cone: (UPE 2014) Um torneiro mecânico construiu uma peça retirando, de um cilindro metálico maciço, uma forma cônica, de acordo com a figura 01 a seguir:
Considere π ≈ 3
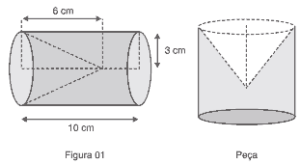
Qual é o volume aproximado da peça em milímetros cúbicos?
a) 2,16 × 105
b) 8,32 × 104
c) 7,2 × 104
d) 3,14 × 105
e) 2,8 × 105
Questão 02. (UEMG 2014) Uma empresa deseja fabricar uma peça maciça cujo formato é um sólido de revolução obtido pela rotação de um trapézio isósceles em torno da base menor, como mostra a figura a seguir. As dimensões do trapézio são: base maior igual a 15 cm, base menor igual a 7 cm e altura do trapézio igual a 3 cm.
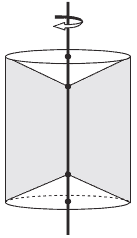
Considerando-se π = 3, o volume, em litros, da peça fabricada corresponde a:
a) 0,212.
b) 0,333.
c) 0,478.
d) 0,536.
Questão 03. (UFG 2013) Um chapeuzinho, distribuído em uma festa, tem a forma de um cone circular reto e, quando planificado, fornece um semicírculo com 10 cm de raio. Para o cone, que representa o formato do chapeuzinho,
a) o raio da base é 10 cm.
b) a área da base é 50pcm2.
c) a área lateral é 25pcm2.
d) a geratriz mede 5 cm.
e) o volume é cm3.
Questão 04 sobre Área e Volume do Cone: (PUC – RS 2013) Um desafio matemático construído pelos alunos do Curso de Matemática tem as peças no formato de um cone. A figura abaixo representa a planificação de uma das peças construídas.
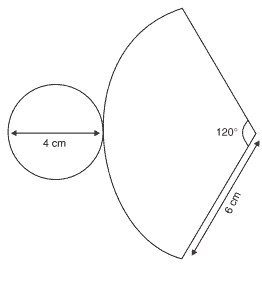
A área dessa peça é de ______ cm2.
a) 10π
b) 16π
c) 20π
d) 28π
e) 40π
Questão 05. (PUC – SP) A altura e o raio da base de um cone circular reto medem 4 cm e 15 cm, respectivamente. Aumentando-se a altura e diminuindo-se o raio da base desse cone, de mesma medida x (x ≠ 0), para obter-se outro cone circular reto de mesmo volume que o original. Determine x, em centímetros.
Questão 06. Com um semicírculo de papel, de raio igual a 20 cm, um vendedor de amendoim faz saquinhos para vender seu produto na forma de cone circular reto. O volume destes saquinhos é:
Dados: π = 3 e √3 = 1,7
a) 1.100 cm3
b) 1.300 cm3
c) 1.500 cm3
d) 1.700 cm3
e) 1.900 cm3
Questão 07 sobre Área e Volume do Cone: (UERJ) Para revestir externamente chapéus em forma de cones com 12 cm de altura e diâmetro da base medindo 10cm, serão utilizados cortes retangulares de tecido, cujas medidas são 67 cm por 50 cm. Admita que todo o tecido de cada corte poderá ser aproveitado. O número mínimo dos referidos cortes necessários para forrar 50 chapéus é igual a:
(Adote π = 3).
a) 3
b) 4
c) 5
d) 6
Questão 08. (FGV 2012) Um ralador de queijo tem a forma de cone circular reto de raio da base 4 cm e altura 10 cm. O queijo é ralado na base do cone e fica acumulado em seu interior (figura 1). Deseja-se retirar uma fatia de um queijo com a forma de cilindro circular reto de raio da base 8 cm e altura 6 cm, obtida por dois cortes perpendiculares à base, partindo do centro da base do queijo e formando um ângulo a (figura 2), de forma que o volume de queijo dessa fatia corresponda a 90% do volume do ralador.
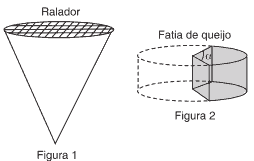
Nas condições do problema, a é igual a:
a) 45°.
b) 50°.
c) 55°.
d) 60°.
e) 65°.
Questão 09. (Enem cancelado 2009) Um vasilhame na forma de um cilindro circular reto de raio da base de 5 cm e altura de 30 cm está parcialmente ocupado por cm3 de álcool. Suponha que sobre o vasilhame seja fixado um funil na forma de um cone circular reto de raio da base de 5 cm e altura de 6 cm, conforme ilustra a figura 1. O conjunto, como mostra a figura 2, é virado para baixo, sendo H a distância da superfície do álcool até o fundo do vasilhame.
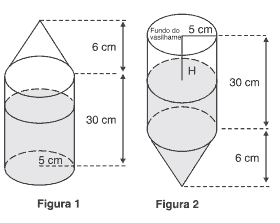
Considerando-se essas informações, qual é o valor da distância H?
a) 5 cm.
b) 7 cm.
c) 8 cm.
d) 12 cm.
e) 18 cm.
Questão 10 sobre Área e Volume do Cone: (UPE 2011) Ao se planificar um cone reto, sua superfície lateral é igual a um quarto de um círculo com área igual a 12π. Nessas condições, a área de sua base é igual a:
a) π.
b) 2π.
c) 3π.
d) 4π.
e) 5π.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas das atividades de matemática sobre Área e Volume do Cone:
1) a;
2) b;
3) e;
4) b;
5) x = 5 cm;
6) d;
7) a;
8) a;
9) b;
10) c
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
