Questão 01. (PUC-SP) Sistemas Lineares Exercícios: Se a, b, c é solução do sistema linear ![]() , então a + b + c é:
, então a + b + c é:
A) –2
B) –1
C) 0
D) 1
E) 2
Questão 02. (UFJF-MG–2007) Resolvendo o sistema de equações lineares 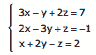 encontramos y igual a:
encontramos y igual a:
A) 1
B) 3
C) 5
D) 2
E) 4
Questão 03. (UFTM-MG–2006) O valor de m para o qual a equação matricial ![]() admite mais de uma solução é um:
admite mais de uma solução é um:
A) divisor negativo de 12.
B) divisor negativo de 25.
C) divisor positivo de 18.
D) múltiplo negativo de 2.
E) múltiplo positivo de 5.
Questão 04. (FGV-SP–2010) Sistemas Lineares Exercícios: Ao resolver o sistema linear determinado a seguir:
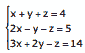
encontramos como solução a tripla ordenada (a, b, c).
O valor de a é:
A) 2
B) 3
C) 0
D) 1
E) –1
Questão 05. (CEFET-MG–2010) Sobre o sistema de equações lineares
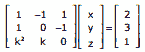
nas variáveis x, y e z, é INCORRETO afirmar que admite:
A) solução para todo k > 0.
B) solução para todo k ∈ (–2, 0).
C) solução para todo k ∈ [–2, –1].
D) única solução para todo k < –2.
E) única solução para todo k ∈ {–1, 2}.
Questão 06. (FGV-SP–2007) A condição necessária e suficiente para que a representação gráfica no plano cartesiano das equações do sistema linear ![]() , nas incógnitas x e y, seja um par de retas paralelas coincidentes é:
, nas incógnitas x e y, seja um par de retas paralelas coincidentes é:
A) m ≠ –2 e n ≠ –3
B) m ≠ –2 e n = –3
C) m = –2
D) m = –2 e n ≠ –3
E) m = –2 e n = –3
Questão 07. (UFOP-MG–2008) Sistemas Lineares Exercícios: Considere o seguinte sistema linear:
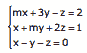
Os valores de m para os quais a solução seja única são:
A) m = –2 ou m = 5
B) m = 2 ou m = –5
C) m ≠ –2 ou m ≠ 5
D) m ≠ 2 ou m ≠ –5
Questão 08. (UFTM-MG–2007) Considere o sistema linear, descrito na forma matricial:
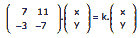
Ele admitirá mais de uma solução para certos valores de k. O produto desses valores de k é:
A) –49
B) –36
C) –25
D) –16
E) –9
Questão 09. (UFJF-MG) Os valores de a e b para que o sistema 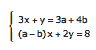 seja possível e indeterminado são:
seja possível e indeterminado são:
A) 3 e 5
B) –2 e 1
C) 1 2 e 3
D) 0 e 1
E) 4 e –2
Questão 10. (Unimontes-MG–2007) O conjunto solução do sistema de equações lineares 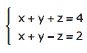 é dado por:
é dado por:
A) {(x, –x + 3,1) | x ∈ }
B) {(x, x – 3, –x) | x ∈ }
C) {(–x, x + 4, –1) | x ∈ }
D) {(–2x, 3x – 1, 4x) | x ∈ }
Questão 11. (Unimontes-MG–2007) Se x = x0, y = y0 e z = z0 são as soluções do sistema de equações lineares 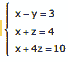 , então x 0 + y0 + z0 é igual a:
, então x 0 + y0 + z0 é igual a:
A) 4
B) 5
C) 3
D) 2
Questão 12. (IME-RJ–2007) Sistemas Lineares Exercícios: Considere o sistema de equações dado por:
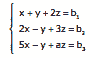
Sendo b1, b2 e b3 valores reais quaisquer, a condição para que o sistema possua solução única é:
A) a = 0
B) a ≠ 2
C) a ≠ 8
D) a ≠ b1 + b2 – b3
E) a = 2b1 + b2 + 3b3
Questão 13. (UFRGS–2006) O sistema
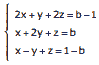
tem solução se, e somente se, b for igual a:
A) –2
B) –1
C) 0
D) 1
E) 2
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos 13 exercícios de matemática sobre Sistemas Lineares Exercícios:
01. D;
02. D;
03. A;
04. B;
05. C;
06. E;
07. C;
08. D;
09. E;
10. A;
11. C;
12. C;
13. E
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
