Questão 01 sobre Teoremas de Pascal e Arquimedes: (UFV-MG–2009) A figura a seguir ilustra uma pessoa equilibrando um caminhão por meio de um elevador hidráulico. O caminhão tem 10 toneladas de massa e está apoiado sobre um pistão cuja a área é de 6 m2. Sabendo que a área do pistão no qual a pessoa atua é de 30 cm2, é CORRETO afirmar que o valor do módulo da força que esta pessoa exerce sobre o pistão é de:
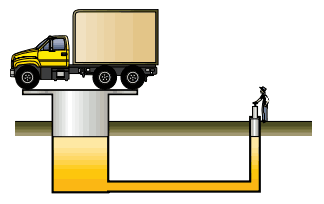
Considere a aceleração da gravidade local g = 10 m/s2.
A) 50 N.
B) 150 N.
C) 200 N.
D) 500 N.
Questão 02. (UFES) A tubulação da figura a seguir contém um líquido incompressível que está retido pelo êmbolo 1 (de área igual a 10,0 cm2) e pelo êmbolo 2 (de área igual a 40,0 cm2). Se a força F1 tem módulo igual a 2,0 N, a força F2, que mantém o sistema em equilíbrio, tem módulo igual a:

A) 0,5 N.
B) 2,0 N.
C) 8,0 N.
D) 500,0 N.
E) 800,0 N.
Questão 03. (PUC RS) Um objeto flutua na água com metade do seu volume imerso, conforme indica a figura.

A respeito desse experimento, pode-se afirmar que:
A) o empuxo da água sobre o objeto tem intensidade igual à metade do peso do objeto.
B) o volume da água deslocada pelo objeto é igual ao volume do objeto.
C) a massa da água deslocada é igual à metade da massa do objeto.
D) o peso da água deslocada tem intensidade igual ao peso do objeto.
E) o empuxo tem intensidade igual à metade do peso da água deslocada.
Questão 04 sobre Teoremas de Pascal e Arquimedes: (Unimontes-MG) Na figura a seguir, estão representados os blocos 1, 2 e 3, de respectivas densidades ρ1, ρ2, ρ3, em um tanque com água, de densidade ρA. Os blocos estão em repouso.
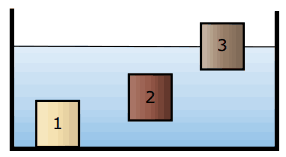
Considere os seguintes conjuntos de relações entre a densidade de cada bloco e a da água do tanque:
I. ρ1 > ρA , ρ2 > ρA , ρ3 < ρA
II. ρ1 = ρA , ρ2 = ρA , ρ3 < ρA
III. ρ1 > ρA , ρ2 = ρA , ρ3 < ρA
Marque a alternativa que indica o(s) conjunto(s) cujas relações entre as densidades estão CORRETAS, de acordo com a situação descrita.
A) I, apenas
B) II, apenas
C) II e III, apenas
D) I e III, apenas
Questão 05. (PUC Minas) Um bloco de madeira flutua em equilíbrio numa porção de água, com apenas uma parte de seu volume mergulhada. Sejam ρA a densidade da água, ρM a densidade da madeira que constitui o bloco, VE o volume da porção do bloco que está acima do nível da água (parte emersa) e V o volume total do bloco. A razão VE/V é:
A) ρM/ρA.
B) (ρA – ρM)/ρA.
C) (ρA – ρM)/ρM.
D) ρA/ρM.
Questão 06. (FGV-SP–2010) Quando você coloca um ovo de galinha dentro de um recipiente contendo água doce, observa que o ovo vai para o fundo, lá permanecendo submerso. Quando, entretanto, você coloca o mesmo ovo dentro do mesmo recipiente agora contendo água saturada de sal de cozinha, o ovo flutua parcialmente. Se, a partir dessa última situação, você colocar suavemente, sem agitação, água doce sobre a água salgada, evitando que as águas se misturem, o ovo, que antes flutuava parcialmente, ficará completamente submerso, porém, sem tocar o fundo.

Com respeito a essa última situação, analise:
I. A densidade da água salgada é maior que a do ovo que, por sua vez, tem densidade menor que a da água doce.
II. O empuxo exercido sobre o ovo é uma força que se iguala, em módulo, ao peso do volume de água doce e salgada que o ovo desloca.
III. A pressão atmosférica afeta diretamente o experimento, de tal forma que, quando a pressão atmosférica aumenta, mesmo que a água se comporte como um fluido ideal, o ovo tende a ficar mais próximo do fundo do recipiente.
É CORRETO o contido em:
A) I, apenas.
B) II, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.
Questão 07 sobre Teoremas de Pascal e Arquimedes: (UFMG) A figura I mostra uma vasilha, cheia de água até a borda, sobre uma balança. Nessa situação, a balança registra um peso P1. Um objeto de peso P2 é colocado nessa vasilha e flutua, ficando parcialmente submerso, como mostra a figura II. Um volume de água igual ao volume da parte submersa do objeto cai para fora da vasilha.
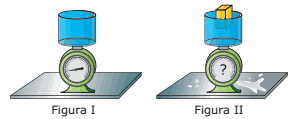
Com base nessas informações, é CORRETO afirmar que, na figura II, a leitura da balança é:
A) igual a P1.
B) igual a P1 + P2.
C) maior que P1 e menor que P1 + P2.
D) menor que P1.
Questão 08. (UERJ–2010) Uma pessoa totalmente imersa em uma piscina sustenta, com uma das mãos, uma esfera maciça de diâmetro igual a 10 cm, também totalmente imersa. Observe a ilustração.

A massa específica do material da esfera é igual a 5,0 g/cm3 e a da água da piscina é igual a 1,0 g/cm3. A razão entre a força que a pessoa aplica na esfera para sustentá-la e o peso da esfera é igual a:
A) 0,2.
B) 0,4.
C) 0,8.
D) 1,0.
Questão 09. (UFMG) De uma plataforma com um guindaste, faz-se descer lentamente e com velocidade constante um bloco cilíndrico de concreto para dentro da água.
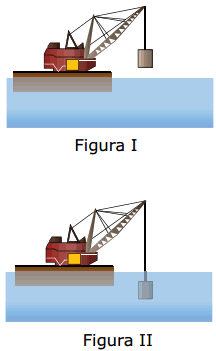
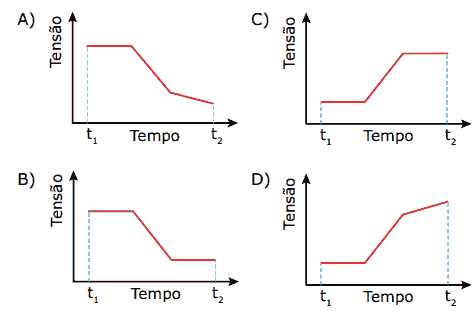
Na figura I, está representado o bloco, ainda fora da água, em um instante t1 e, na figura II, o mesmo bloco, em um instante t2 posterior, quando já está dentro da água. Assinale a alternativa cujo gráfico MELHOR representa a tensão no cabo do guindaste em função do tempo.
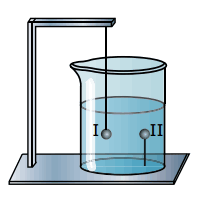
Questão 10 sobre Teoremas de Pascal e Arquimedes: (UFMG) Na figura, estão representadas duas esferas, I e II, de mesmo raio, feitas de materiais diferentes e imersas em um recipiente contendo água. As esferas são mantidas nas posições indicadas por meio de fios que estão tensionados.

Com base nessas informações, é CORRETO afirmar que o empuxo:
A) é igual à tensão no fio para as duas esferas.
B) é maior na esfera de maior massa.
C) é maior que o peso na esfera I.
D) é maior que o peso na esfera II.
🔵 >>> Verifique todos os nossos exercícios e atividades de Física.
Gabarito com as respostas dos 10 exercícios de Física sobre Teoremas de Pascal e Arquimedes:
01. A;
02. C;
03. D;
04. C;
05. B;
06. B;
07. A;
08. C;
09. C;
10. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
