Questão 01 sobre Probabilidade Matemática: Modelo Enem. A figura I abaixo mostra um esquema das principais vias que interligam a cidade A com a cidade B. Cada número indicado na figura II representa a probabilidade de pegar um engarrafamento quando se passa na via indicada, Assim, há uma probabilidade de 30% de se pegar engarrafamento no deslocamento do ponto C ao o ponto B, passando pela estrada E4, e de 50%, quando se passa por E3. Essas probabilidades são independentes umas das outras.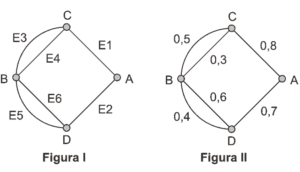
Paula deseja se deslocar da cidade A para a cidade B usando exatamente duas das vias indicadas, percorrendo um trajeto com a menor probabilidade de engarrafamento possível. O melhor trajeto para Paula é:
a) E1E3.
b) E1E4.
c) E2E4.
d) E2E5.
e) E2E6.
Questão 02 sobre Probabilidade Matemática: O diretor de um colégio leu numa revista que os pés das mulheres estavam aumentando. Há alguns anos, a média do tamanho dos calçados das mulheres era de 35,5 e, hoje, é de 37,0. Embora não fosse uma informação científica, ele ficou curioso e fez uma pesquisa com as funcionárias do seu colégio, obtendo o quadro a seguir:
| TAMANHO DOS CALÇADOS | NUMERO DE FUNCIONÁRIAS |
| 39,0 | 1 |
| 38,0 | 10 |
| 37,0 | 3 |
| 36,0 | 5 |
| 35,0 | 6 |
Escolhendo uma funcionária ao acaso e sabendo que ela tem calcado maior que 36,0, a probabilidade de ela calçar 38,0 é
Questão 03. O controle de qualidade de uma empresa fabricante de telefones celulares aponta que a probabilidade de um aparelho de determinado modelo apresentar defeito de fabricação é de 0,2%. Se uma loja acaba de vender 4 aparelhos desse modelo para um cliente, qual é a probabilidade de esse cliente sair da loja com exatamente dois aparelhos defeituosos?
a) 2 × (0,2%)4.
b) 4 × (0,2%)2.
c) 6 × (0,2%)2 × (99,8%)2.
d) 4 × (0,2%).
e) 6 × (0,2%) × (99,8%).
Questão 04 sobre Probabilidade Matemática: Um médico está estudando um novo medicamento que combate um tipo de câncer em estágios avançados. Porém, devido ao forte efeito dos seus componentes, a cada dose administrada há uma chance de 10% de que o paciente sofra algum dos efeitos colaterais observados no estudo, tais como dores de cabeça, vômitos ou mesmo agravamento dos sintomas da doença. O médico oferece tratamentos compostos por 3, 4, 6, 8 ou 10 doses do medicamento, de acordo com o risco que o paciente pretende assumir.
Se um paciente considera aceitável um risco de até 35% de chances de que ocorra algum dos efeitos colaterais durante o tratamento, qual é o maior número admissível de doses para esse paciente?
a) 3 doses.
b) 4 doses.
c) 6 doses.
d) 8 doses.
e) 10 doses.
Questão 05. A vida na rua como ela é O Ministério do Desenvolvimento Social e Combate à Fome (MDS) realizou, em parceria com a ONU, uma pesquisa nacional sobre a população que vive na rua, tendo sido ouvidas 31.922 pessoas em 71 cidades brasileiras. Nesse levantamento, constatou-se que a maioria dessa população sabe ler e escrever (74%), que apenas 15,1% vivem de esmolas e que, entre os moradores de rua que ingressaram no ensino superior, 0,7% se diplomou. Outros dados da pesquisa são apresentados nos quadros a seguir.
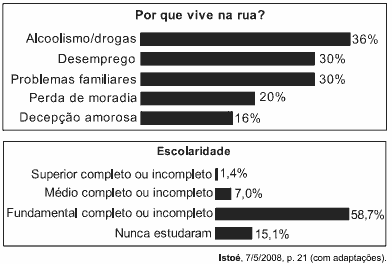
No universo pesquisado, considere que P seja o conjunto das pessoas que vivem na rua por motivos de alcoolismo/drogas e Q seja o conjunto daquelas cujo motivo para viverem na rua é a decepção amorosa. Escolhendo-se ao acaso uma pessoa no grupo pesquisado e supondo-se que seja igual a 40% a probabilidade de que essa pessoa faça parte do conjunto P ou do conjunto Q , então a probabilidade de que ela faça parte do conjunto interseção de P e Q é igual a
a) 12%.
b) 16%.
c) 20%.
d) 36%.
e) 52%.
Questão 06 sobre Probabilidade Matemática: A queima de cana aumenta a concentração de dióxido de carbono e de material particulado na atmosfera, causa alteração do clima e contribui para o aumento de doenças respiratórias. A tabela adiante apresenta números relativos a pacientes internados em um hospital no período da queima da cana.
| pacientes | problemas respiratórios causados pelas queimadas | problemas respiratórios resultantes de outras causas | outras doenças | total |
| idosos | 50 | 150 | 60 | 260 |
| crianças | 150 | 210 | 90 | 450 |
Escolhendo-se aleatoriamente um paciente internado nesse hospital por problemas respiratórios causados pelas queimadas, a probabilidade de que ele seja uma criança é igual a
a) 0,26, o que sugere a necessidade de implementação de medidas que reforcem a atenção ao idoso internado com problemas respiratórios.
b) 0,50, o que comprova ser de grau médio a gravidade dos problemas respiratórios que atingem a população nas regiões das queimadas.
c) 0,63, o que mostra que nenhum aspecto relativo à saúde infantil pode ser negligenciado.
d) 0,67, o que indica a necessidade de campanhas de conscientização que objetivem a eliminação das queimadas.
e) 0,75, o que sugere a necessidade de que, em áreas atingidas pelos efeitos das queimadas, o atendimento hospitalar no setor de pediatria seja reforçado.
Questão 07 sobre Probabilidade Matemática:
Uma das principais causas da degradação de peixes frescos é a contaminação por bactérias. O gráfico apresenta resultados de um estudo acerca da temperatura de peixes frescos vendidos em cinco peixarias. O ideal é que esses peixes sejam vendidos com temperaturas entre 2º C e 4º C. Selecionando-se aleatoriamente uma das cinco peixarias pesquisadas, a probabilidade de ela vender peixes frescos na condição ideal é igual a
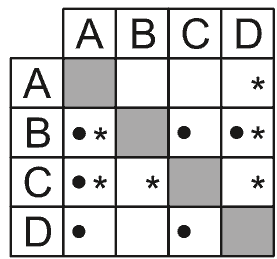
Questão 08 sobre Probabilidade Matemática: Modelo Enem. A tabela a seguir indica a posição relativa de quatro times de futebol na classificação geral de um torneio, em dois anos consecutivos. O símbolo • significa que o time indicado na linha ficou, no ano de 2004, à frente do indicado na coluna. O símbolo * significa que o time indicado na linha ficou, no ano de 2005, à frente do indicado na coluna.
A probabilidade de que um desses quatro times, escolhido ao acaso, tenha obtido a mesma classificação no torneio, em 2004 e 2005, é igual a
a) 0,00.
b) 0,25.
c) 0,50.
d) 0,75.
e) 1,00.
Questão 09. Modelo Enem. Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o prêmio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas casas. Na discussão para se decidir com quem ficaria o troféu, travou-se o seguinte diálogo:
Pedro, camisa 6: — Tive uma ideia. Nós somos 11 jogadores e nossas camisas estão numeradas de 2 a 12. Tenho dois dados com as faces numeradas de 1 a 6. Se eu jogar os dois dados, a soma dos números das faces que ficarem para cima pode variar de 2 (1 + 1) até 12 (6 + 6). Vamos jogar os dados, e quem tiver a camisa com o número do resultado vai guardar a taça. Tadeu, camisa 2: – Não sei não… Pedro sempre foi muito esperto… Acho que ele está levando alguma vantagem nessa proposta… Ricardo, camisa 12: – Pensando bem… Você pode estar certo, pois, conhecendo o Pedro, é capaz que ele tenha mais chances de ganhar que nós dois juntos…
Desse diálogo conclui-se que
a) Tadeu e Ricardo estavam equivocados, pois a probabilidade de ganhar a guarda da taça era a mesma para todos.
b) Tadeu tinha razão e Ricardo estava equivocado, pois, juntos, tinham mais chances de ganhar a guarda da taça do que Pedro.
c) Tadeu tinha razão e Ricardo estava equivocado, pois, juntos, tinham a mesma chance que Pedro de ganhar a guarda da taça.
d) Tadeu e Ricardo tinham razão, pois os dois juntos tinham menos chances de ganhar a guarda da taça do que Pedro.
e) não é possível saber qual dos jogadores tinha razão, por se tratar de um resultado probabilístico, que depende exclusivamente da sorte.
Questão 10 sobre Probabilidade Matemática: Modelo Enem. Um aluno de uma escola será escolhido por sorteio para representá-la em uma certa atividade. A escola tem dois turnos. No diurno há 300 alunos, distribuídos em 10 turmas de 30 alunos. No noturno há 240 alunos, distribuídos em 6 turmas de 40 alunos. Em vez do sorteio direto envolvendo os 540 alunos, foram propostos dois outros métodos de sorteio:
Método I: escolher ao acaso um dos turnos (por exemplo, lançando uma moeda) e, a seguir, sortear um dos alunos do turno escolhido.
Método II: escolher ao acaso uma das 16 turmas (por exemplo, colocando um papel com o número de cada turma em uma urna e sorteando uma delas) e, a seguir, sortear um dos alunos dessa turma.
Sobre os métodos I e II de sorteio é correto afirmar:
a) em ambos os métodos, todos os alunos têm a mesma chance de serem sorteados.
b) no método I, todos os alunos têm a mesma chance de serem sorteados, mas, no método II a chance de um aluno do diurno ser sorteado é maior que a de um aluno do noturno.
c) no método II, todos os alunos têm a mesma chance de serem sorteados, mas, no método I, a chance de um aluno do diurno ser sorteado é maior que a de um aluno do noturno.
d) no método I, a chance de um aluno do noturno ser sorteado é maior do que a de um aluno do diurno, enquanto no método II ocorre o contrário.
e) em ambos os métodos, a chance de um aluno do diurno ser sorteado é maior do que a de um aluno do noturno.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos melhores 10 exercícios sobre Probabilidade Matemática:
01. D
Probabilidade de congestionamento = 1 – probabilidade de não haver congestionamento
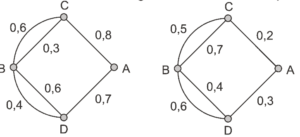
E1E3 =1-0,2.0,5 = 0,9
E1E4 = 1 -0,2.0,7 = 0,86
E2E5 = 1 – 0,3.0,6 = 0,82 (menor probabilidade)
E2E5 = 1 – 0,3.0,4 = 0,88
O trajeto E2E4 não existe.
02. D
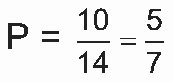
03. C
04. B
3 doses → (1- 0,93).100% = 27%
4 doses → (1- 0,94).100% = 34%
5 doses → (1- 0,95).100% = 41%
Resposta 4 doses.
05. A
Queremos calcular P(P ∩ Q).
Aplicando o Teorema da Soma obtemos
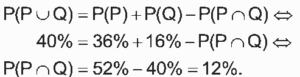
06. E
Sejam os eventos A : “criança” e B : “tem problema respiratório causado pelas queimadas”. Queremos calcular P(A | B), ou seja, a probabilidade condicional de A dado B. Temos que
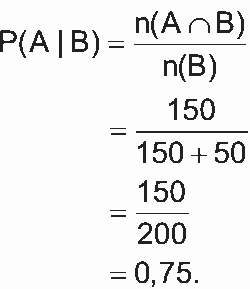
07. D
De acordo com o gráfico, a única peixaria que vende peixes frescos na condição ideal é a V.
Portanto, a probabilidade pedida é 
08. A
De acordo com as informações do enunciado, podemos construir a seguinte tabela:
| Posição | 2004 | 2005 |
| 1º | B | C |
| 2º | D | B |
| 3º | C | A |
| 4º | A | D |
Portanto, como nenhum dos times obteve a mesma classificação no torneio em 2004 e 2005, segue que a probabilidade pedida vale zero (evento impossível).
09. D
O espaço amostral do lançamento dos dois dados é
Desse modo, como a soma dos dados é igual a 6 em (5,1), (4, 2), (3, 3), (2, 4) e (1, 5), segue que a probabilidade de Pedro ganhar o sorteio é 
. Por outro lado, os únicos resultados favoráveis a Tadeu e Ricardo são, respectivamente, (1,1) e (6, 6). Logo, a probabilidade de Tadeu ou Ricardo ficarem com a taça é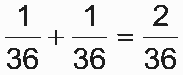 
. Portanto, como 
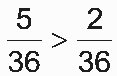Tadeu e Ricardo tinham razão, pois os dois juntos tinham menor probabilidade de ganhar a guarda da taça do que Pedro.
10.D
No método I, a probabilidade de um aluno do turno diurno ser sorteado é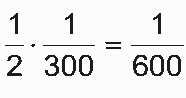 
enquanto que a probabilidade de um aluno do turno noturno ser sorteado é 
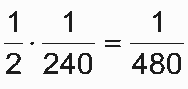No método II, a probabilidade de um aluno do turno diurno ser sorteado é 
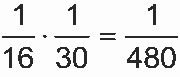enquanto que a probabilidade de um aluno do turno noturno ser sorteado é 
.
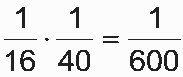Portanto, no método I, a probabilidade de um aluno do noturno ser sorteado é maior do que a de um aluno do diurno, enquanto no método II ocorre o contrário.
Observação: Chance de ocorrência de um evento é a razão entre a probabilidade de sua ocorrência e a probabilidade de sua não ocorrência. Desse modo, chance e probabilidade não são sinônimos.
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína