Questão 01 sobre Conjuntos Numéricos: (UFJF-MG) Marque a alternativa INCORRETA a respeito dos números reais.
A) Se a representação decimal infinita de um número é periódica, então esse número é racional.
B) Se a representação decimal de um número é finita, então esse número é racional.
C) Todo número irracional tem uma representação decimal infinita.
D) Todo número racional tem uma representação decimal finita.
Questão 02. Modelo Enem. Assinale a afirmativa VERDADEIRA.
A) A soma de dois números irracionais positivos é um número irracional.
B) O produto de dois números irracionais distintos é um número irracional.
C) O quadrado de um número irracional é um número racional.
D) A raiz quadrada de um número racional é um número irracional.
E) A diferença entre um número racional e um número irracional é um número irracional.
Questão 03. (UFOP-MG–2009) A respeito dos números a = 0,499999… e b = 0,5, é CORRETo afirmar:
A) b = a + 0,011111…
B) a = b
C) a é irracional e b é racional.
D) a < b
Questão 04 sobre Conjuntos Numéricos: (UFJF-MG) Dados os intervalos A = [–1, 3), B = [1, 4], C = [2, 3), D = (1, 2] e E = (0, 2], consideremos o conjunto P = [(A ∪ B) – (C ∩ D)] – E. Marque a alternativa INCORRETA.
A) P ⊂ [–1, 4]
B) (3, 4] ⊂ P
C) 2 ∈ P
D) 0 ∈ P
Questão 05. (Fatec–SP) Sejam a e b números irracionais.
Das afirmações:
I. ab é um número irracional.
II. a + b é um número irracional.
III. a – b pode ser um número irracional.
Pode-se concluir que:
A) as três são falsas.
B) as três são verdadeiras.
C) somente I e III são verdadeiras.
D) somente I é verdadeira.
E) somente I e II são falsas.
Questão 06. (PUC-SP) Um número racional qualquer:
A) tem sempre um número finito de ordens (casas) decimais.
B) tem sempre um número infinito de ordens (casas) decimais.
C) não pode expressar-se na forma decimal exata.
D) nunca se expressa na forma de uma decimal inexata.
E) N.d.a.
Questão 07 sobre Conjuntos Numéricos: (UFJF-MG) Marque a alternativa INCORRETA.
A) Se x e y são números racionais, então x + y é um número racional.
B) Se x e y são números irracionais, então x + y é um número irracional.
C) Se x e y são números racionais, então xy é um número racional.
D) Se x é um número racional e y é um número irracional, então x + y é um número irracional.
Questão 08. (FUVEST-SP) Na figura, estão representados geometricamente os números reais 0, x, y e 1. Qual a posição do número xy?

A) À esquerda de 0.
B) Entre 0 e x.
C) Entre x e y.
D) Entre y e 1.
E) À direita de 1.
Questão 09. (Enem–2009) A Música e a Matemática se encontram na representação dos tempos das notas musicais, conforme a figura seguinte:
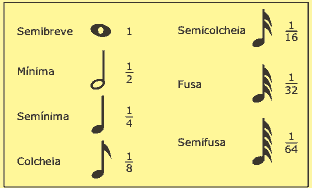
Um compasso é uma unidade musical composta de determinada quantidade de notas musicais em que a soma das durações coincide com a fração indicada como fórmula do compasso. Por exemplo, se a fórmula de compasso for , poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, sendo possível a combinação de diferentes figuras. Um trecho musical de oito compassos, cuja fórmula é
, poderia ser preenchido com:
A) 24 fusas.
B) 3 semínimas.
C) 8 semínimas.
D) 24 colcheias e 12 semínimas.
E) 16 semínimas e 8 semicolcheias.
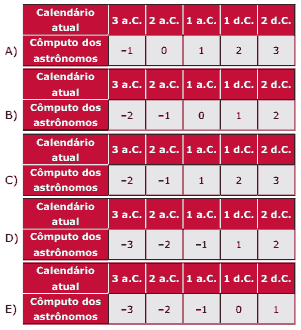
Questão 10 sobre Conjuntos Numéricos: (Enem–2009 / Anulada) No calendário utilizado atualmente, os anos são numerados em uma escala sem o zero, isto é, não existe o ano zero. A Era Cristã se inicia no ano 1 depois de Cristo (d.C.) e designa-se o ano anterior a esse como ano 1 antes de Cristo (a.C.). Por essa razão, o primeiro século ou intervalo de 100 anos da era cristã terminou no dia 31 de dezembro do ano 100 d.C., quando haviam decorrido os primeiros 100 anos após o início da era. O século II começou no dia 1 de janeiro do ano 101 d.C., e assim sucessivamente. Como não existe o ano zero, o intervalo entre os anos 50 a.C. e 50 d.C., por exemplo, é de 100 anos. Outra forma de representar anos é utilizando-se números inteiros, como fazem os astrônomos. Para eles, o ano 1 a.C. corresponde ao ano 0, o ano 2 a.C. ao ano -1, e assim sucessivamente.
Os anos depois de Cristo são representados pelos números inteiros positivos, fazendo corresponder o número 1 ao ano 1 d.C. Considerando o intervalo de 3 a.C. a 2 d.C., o quadro que relaciona as duas contagens descritas no texto é:
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas do simulado com 10 questões de matemática sobre Conjuntos Numéricos:
01. D;
02. E;
03. B;
04. C;
05. E;
06. E;
07. B;
08. B;
09. D;
10. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
