Determinantes e Matrizes Inversas 10 Exercícios

Questão 01 sobre Determinantes e Matrizes Inversas: (FEI-SP) Para que o determinante da matriz seja nulo, o valor de a deve ser:

a) 2 ou -2.
b) 1 ou 3.
c) –3 ou 5.
d) –5 ou 3.
e) 4 ou –4.

Questão 02. (Vunesp) Considere a matriz A = (aij) 2 x 2, defnida por aij = –1 + 2i + j, para 1 ≤ i ≤ 2, 1 ≤ j ≤ 2. O determinante de A é:

a) 22.
b) 2.
c) 4.
d) –2.
e) –4.

Questão 03. (UEL-PR) A soma dos determinantes, indicados a seguir, é igual a zero

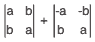
a) quaisquer que sejam os valores reais de a e de b.
b) se, e somente se, a = b.
c) se, e somente se, a = –b.
d) se, e somente se, a = 0.
e) se, e somente se, a = b = 1.

Questão 04 sobre Determinantes e Matrizes Inversas: (UFMG) O produto das raízes da equação 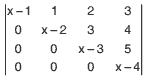= 0 é igual a:

a) 0.
b) 6.
c) 12.
d) 24.
e) -24.

Questão 05. (FGV-SP) O determinante é igual a:

a) 0.
b) -55.
c) 55.
d) -250.
e) 250.

Questão 06. (ITA-SP) Sendo A uma matriz quadrada de ordem 3, cujo determinante é igual a 4, qual o valor de x na equação det (2A . At) = 4x?

a) 4.
b) 8.
c) 16.
d) 32.
e) n.d.a.

Questão 07 sobre Determinantes e Matrizes Inversas: (Vunesp) Se o determinante de uma matriz quadrada A, de ordem 3, é 5, então o determinante da matriz 4A é igual a:

a) 320.
b) 100.
c) 60.
d) 15.
e) 5.

Questão 08. (PUC-MG) M é uma matriz quadrada de ordem 3, e seu determinante é 2. O valor da expressão det(M) + det(2M) + det(3M) :é

a) 12.
b) 15.
c) 36.
d) 54.
e) 72.

Questão 09. (UFGO) A e B são matrizes quadradas de ordem 3, tais que At – 2B = O3 e det B = 1. Então, det A é igual a:

a) 2.
b) 4.
c) 6.
d) 8.
e) -8.

Questão 10 sobre Determinantes e Matrizes Inversas: (Fuvest) Se A é uma matriz 2 x 2 invertível que satisfaz A2 = 2A, então o determinante de A será:

a) 0.
b) 1.
c) 2.
d) 3.
e) 4.

🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.

Gabarito com as respostas do simulado com 10 exercícios de Matemática sobre Determinantes e Matrizes Inversas:

01) a;

02) d;

03) a;

04) d;

05) e;

06) d;

07) a;

08) e;

09) d;

10) e

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína