Questão 01 sobre Probabilidade Eventos e Amostra: (FUVEST-SP–2009) Dois dados cúbicos, não viciados, com faces numeradas de 1 a 6, serão lançados simultaneamente. A probabilidade de que sejam sorteados dois números consecutivos, cuja soma seja um número primo, é de:
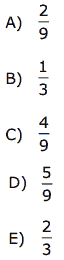
Questão 02. (UFMG–2007) Em uma mesa, estão espalhados 50 pares de cartas. As duas cartas de cada par são iguais e cartas de pares distintos são diferentes. Suponha que duas dessas cartas são retiradas da mesa ao acaso. Então, é CORRETO afirmar que a probabilidade de essas duas cartas serem iguais é:
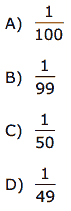
Questão 03. (UFTM-MG–2010) Um saco continha 20 bolas, entre brancas e azuis. Desse modo, havia uma probabilidade p de se retirar ao acaso 1 bola azul. Foram retiradas 2 bolas ao acaso e verificou-se que uma era azul e a outra, branca. A probabilidade de se tirar ao acaso 1 bola azul passou a ser de p – .
O número inicial de bolas azuis no saco era
A) 15
B) 12
C) 8
D) 5
E) 2
Questão 04 sobre Probabilidade Eventos e Amostra: (PUC-SP) Joel e Jane fazem parte de um grupo de dez atores: 4 mulheres e 6 homens. Se duas mulheres e três homens forem escolhidos p
ara compor o elenco de uma peça teatral, a probabilidade de que Joel e Jane, juntos, estejam entre eles é:
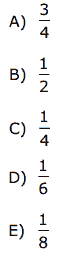
Questão 05. (Unicamp-SP) Uma urna contém 50 bolas que se distinguem apenas pelas seguintes características:
I) x delas são brancas e numeradas sequencialmente com os números naturais de 1 a x.
II) x + 1 delas são azuis e numeradas sequencialmente com os números naturais de 1 a x + 1.
III)x + 2 delas são amarelas e numeradas sequencialmente com os números naturais de 1 a x + 2.
IV) x + 3 delas são verdes e numeradas sequencialmente de 1 a x + 3.
A) Qual é o valor numérico de x?
B) Qual a probabilidade de ser retirada, ao acaso, uma bola azul ou uma bola com o número 12?
Questão 06. (UFU-MG–2006) Numa classe com 50 alunos, 8 serão escolhidos, aleatoriamente, para formar uma comissão eleitoral. A probabilidade de Lourenço, Paulo e Larissa, alunos da classe, fazerem parte desta comissão é igual a:
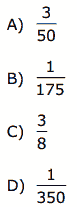
Questão 07 sobre Probabilidade Eventos e Amostra: (Mackenzie-SP) Num grupo de 12 professores, somente 5 são de Matemática. Escolhidos ao acaso 3 professores do grupo, a probabilidade de, no MÁXIMO, um deles ser de Matemática é:
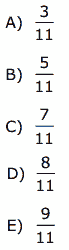
Questão 08. (CEFET-MG–2008) A Coordenação de Matemática de uma escola promoveu uma gincana, na qual uma das tarefas era resolver o seguinte problema:
“As faces de uma moeda são denominadas cara (K) e coroa (C). Se essa moeda for lançada 6 vezes, qual é a probabilidade de se obter 4 caras e 2 coroas?”
A equipe marcaria ponto, nessa tarefa, se encontrasse:
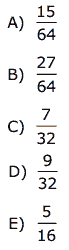
Questão 09. (Mackenzie-SP) Uma pessoa A concorre com você neste Concurso Vestibular com 40% de chance de ser aprovada. A probabilidade de que pelo menos um de vocês dois seja aprovado é 64%. Então, relativamente à pessoa A, a probabilidade de você ser aprovado é:
A) a mesma.
B) o dobro.
C) o triplo.
D) a metade.
E) um quarto.
Questão 10 sobre Probabilidade Eventos e Amostra: (Enem–2001) Um município de 628 km2 é atendido por duas emissoras de rádio cujas antenas A e B alcançam um raio de 10 km do município, conforme mostra a figura.
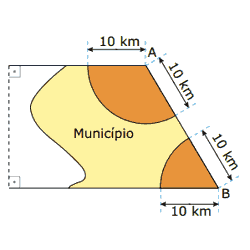
Para orçar um contrato publicitário, uma agência precisa avaliar a probabilidade que um morador tem de, circulando livremente pelo município, encontrar-se na área de alcance de pelo menos uma das emissoras.
Essa probabilidade é de, aproximadamente:
A) 20%.
B) 25%.
C) 30%.
D) 35%.
E) 40%.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos exercícios de Matemática sobre Probabilidade Eventos e Amostra:
01. A;
02. B;
03. D;
04. C;
05. A) x = 11; B)
06. D;
07. C;
08. A;
09. A;
10. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
