Questão 01 sobre Sequências Matemáticas: UFMG. José decidiu nadar, regularmente, de quatro em quatro dias. Começou a fazê-lo em um sábado; nadou pela segunda vez na quarta-feira seguinte e assim por diante.
Nesse caso, na centésima vez em que José for nadar, será:
a) terça-feira.
b) quarta-feira.
c) quinta-feira
d) sexta-feira.
Questão 02. Fatec-SP. Na compra a prazo de um aparelho eletrodoméstico, o total pago por uma pessoa foi R$ 672,00. A entrada teve valor correspondente a 1/6 do total, e o restante foi pago em 4 parcelas, cujos valores formaram uma progressão aritmética crescente de razão R$ 40,00.
O valor da última prestação foi:
a) R$ 220,00
b) R$ 215,00
c) R$ 210,00
d) R$ 205,00
e) R$ 200,00
Questão 03. Fuvest-SP. Uma progressão aritmética e uma progressão geométrica têm ambas, o primeiro termo igual a 4, sendo que os seus terceiros termos são estritamente positivos e coincidem. Sabe-se ainda que o segundo termo da progressão aritmética excede o segundo termo da progressão geométrica em 2. Então, o terceiro termo das progressões é:
a) 10
b) 12
c) 14
d) 16
e) 18
Questão 04 sobre Sequências Matemáticas: FEI-SP. A população atual de roedores em um “lixão” foi estimada em 400, com uma perspectiva de crescimento em progressão geométrica, dobrando a quantidade a cada 6 meses. Admitindo-se que essas estimativas sejam válidas, pode-se afirmar que:
a) em 3 anos a população terá ultrapassado 50000 roedores.
b) em 2 anos a população terá ultrapassado 30000 roedores.
c) em 4 anos a população terá ultrapassado 50000 roedores.
d) em 5 anos a população terá ultrapassado 4000000 roedores.
e) em 1 ano a população terá ultrapassado 5000 roedores.
Questão 05. U.Católica-DF. Um atleta está se preparando para disputar a maratona nos jogos de Sidney. No último treino, a planilha do cronometrista mostrou que, nos primeiros 10 minutos, o atleta havia percorrido 3,5 km. Nos 10 minutos seguintes, 3,4 km; nos 10 minutos a seguir, 3,3 km e assim sucessivamente; 100 metros a menos a cada 10 minutos de corrida.
É correto afirmar que:
a) O atleta levará 3 horas para percorrer 42 km.
b) Nesse último treino, o atleta percorrerá 20 km em 2 horas.
c) O atleta completará os 22 km em 2 horas e 20 minutos.
d) O atleta percorrerá 30 km em 2 horas e 20 minutos.
e) O atleta percorrerá 42 km em 2 horas e 30 minutos.
Questão 06. Unifor-CE. Em um triângulo, as medidas dos ângulos internos estão em progressão aritmética. Se a menor dessas medidas é 10°, a maior delas é:
a) 90°
b) 100°
c) 110°
d) 120°
e) 130°
Questão 07 sobre Sequências Matemáticas: FURG-RS. Em uma progressão aritmética de n termos, sendo n ímpar, o termo central é:
a) a diferença entre os termos extremos divididos por n.
b) a média aritmética entre todos os termos multiplicada por dois.
c) o dobro da soma dos termos divididos por n.
d) a média aritmética de qualquer par de termos equidistantes dos extremos.
e) a soma dos n termos dividida por 2.
Questão 08. U. F. Santa Maria-RS. Tisiu ficou sem parceiro para jogar bolita (bola de gude); então pegou sua coleção de bolitas e formou uma sequência de “T” (a inicial de seu nome), conforme a figura:
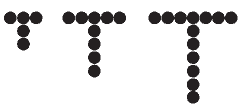
Supondo que o guri conseguiu formar 10 “T” completos, pode-se, seguindo o mesmo padrão, afirmar que ele possuía:
a) mais de 300 bolitas.
b) pelo menos 230 bolitas.
c) menos de 220 bolitas.
d) exatamente 300 bolitas.
e) exatamente 41 bolitas.
Questão 09. PUC-PR. Se dividirmos o décimo primeiro termo de uma progressão aritmética pelo seu terceiro termo, obtemos 4, enquanto, se dividirmos o nono termo da progressão pelo seu quarto termo, obtemos 2 e o resto 4. A soma dos 20 primeiros termos dessa progressão é:
a) 250
b) 430
c) 610
d) 590
e) 820
Questão 10 sobre Sequências Matemáticas: U.Católica Dom Bosco-DF. Na segunda-feira, uma garota conta um segredo a três amigas. Na terça-feira, cada uma dessas amigas conta esse segredo a três outras amigas. E assim, a cada dia, no decorrer da semana, as garotas que ouviram o segredo no dia anterior, contam-no a três outras amigas.
No final da sexta-feira dessa semana, o número de garotas que conhecem o segredo é igual a:
a) 82
b) 121
c) 244
d) 364
e) 1090
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas do simulado com 10 exercícios sobre Sequências Matemáticas:
01. B;
02. E;
03. D;
04. C;
05. E;
06. C;
07. D;
08. B;
09. C;
10. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
