Questão 01 sobre Sistema Cartesiano: (UFMG–2007) Seja P(a, b) um ponto no plano cartesiano, tal que 0 < a < 1 e 0 < b < 1. As retas paralelas aos eixos coordenados que passam por p dividem o quadrado de vértices (0, 0), (2, 0), (0, 2) e (2, 2) nas regiões I, II, III e IV, como mostrado nesta figura:
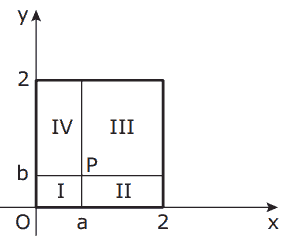
Considere o ponto Q = ( , ab).
Então, é CORRETO afirmar que o ponto Q está na região:
A) I.
B) II.
C) III.
D) IV.
Questão 02. (FUVEST-SP) Sejam A(1, 2) e B(3, 2) dois pontos do plano cartesiano. Nesse plano, o segmento é obtido do segmento
por uma rotação de 60°, no sentido anti-horário, em torno do ponto A. As coordenadas do ponto C são:
A) (2, 2 + √3)
B)
C) (2, 1 + √3)
D) (2, 2 – √3)
E) (1 + √3, 2 + √3)
Questão 03. (Mackenzie-SP–2009)
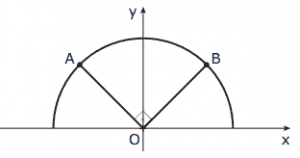
A figura mostra uma semicircunferência com centro na origem. Se o ponto A é (–√2, 2), então o ponto B é:
A) (2, √2)
B) (√2, 2)
C) (1, √5)
D) (√5, 1)
E) (2, √5)
Questão 04 sobre Sistema Cartesiano: (UFMG) A distância entre os pontos A(2a, –3a) e B(3, 2) é √26. Pode-se afirmar que os possíveis valores de a são:
A) –√ e √2
B) 1 – √2 e 1 + √2
C) –1 e 1
D) –2 e 2
E) –3 e 2
Questão 05. (UCSal-BA) Na figura, o triângulo ABC é equilátero, sendo A e B, respectivamente, os pontos (0, 0) e (4, 0).
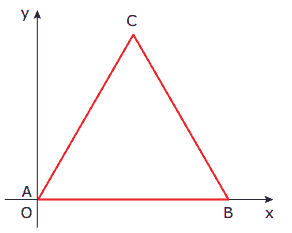
As coordenadas do ponto C são:
A) (2, 1)
B) (2, 2)
C) (2, 2√3)
D) (3, 3√3)
E) (3, 2)
Questão 06. (UFMG–2010) Os pontos A(0, 3), B(4, 0) e C(a, b) são vértices de um triângulo equilátero no plano cartesiano.
Considerando-se essa situação, é CORRETO afirmar que:
A) b = a
B) b = a –
C) b = a + 3
D) b = a –
Questão 07 sobre Sistema Cartesiano: (UFMG) Se A(0, 0), B(1, 0), C(1, 1), D(0, 1) são os vértices de um quadrado, então P pertence:
A) ao lado .
B) ao lado .
C) ao lado .
D) à diagonal .
E) à diagonal .
Questão 08. (UECE) Se o ponto P1(x1, y1) é equidistante dos pontos O(0, 0), M(7, –7) e N(8, 0), então x21 + y21 é igual a:
A) 13
B) 17
C) 25
D) 29
E) N.d.a.
Questão 09. (UFOP-MG–2008) O baricentro de um triângulo é o ponto de encontro de suas medianas. Sendo assim, as coordenadas cartesianas do baricentro do triângulo de vértices (2, 2), (–4, –2) e (2, –4) são:
A)
B)
C)
D)
Questão 10 sobre Sistema Cartesiano: (UFAL) Sejam P(2, 1) e o ponto Q, de abscissa 4, localizado no 1º quadrante. Se a distância de Q a p é igual à distância de Q ao eixo das abscissas, então Q é o ponto:
A)
B)
C) (4, 3)
D) (2, 4)
E) (4, 4)
>>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista com 10 exercícios de matemática sobre o Sistema Cartesiano:
01. B;
02. A;
03. A;
04. C;
05. C;
06. B;
07. D;
08. C;
09. A;
10. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína