Lista com 10 Exercícios sobre Função Exponencial

Questão 01. (UERJ) Exercícios sobre Função Exponencial: Uma empresa acompanha a produção diária de um funcionário recém-admitido, utilizando uma função f(d), cujo valor corresponde ao número mínimo de peças que a empresa espera que ele produza em cada dia (d), a partir da data de sua admissão. Considere o gráfico auxiliar abaixo, que representa a função y = e^x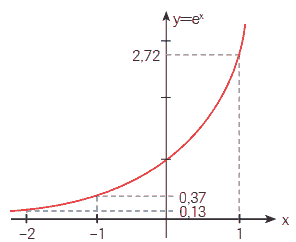

Utilizando f(d) = 100 –100 . e^−0,2d e o gráfico acima, a empresa pode prever que o funcionário alcançará a produção de 87 peças num mesmo dia, quando d for igual a:

a) 5
b) 10
c) 15
d) 20

Questão 02. (UECE) Se x1 e x2 são as raízes da equação 2^x2 . 5^x2= 0,001.(10^3-x)², então + é:

a) 5
b) 10
c) 13
d) 34

Questão 03. (UNIRIO) Uma indústria do Rio de Janeiro libera poluentes na Baía de Guanabara. Foi feito um estudo para controlar essa poluição ambiental, cujos resultados são a seguir relatados:

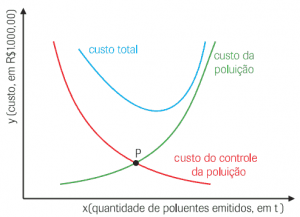
Do ponto de vista da comissão que efetuou o estudo, essa indústria deveria reduzir sua liberação de rejeitos até o nível onde se encontra P, admitindo-se que o custo total ideal é o resultado da adição do custo de poluição y = 2^x −1, ao custo de controle da poluição y = 6 . (1/2)^x. Para que se consiga o custo ideal, a quantidade de poluentes emitidos, em kg, deve ser aproximadamente: (Considere log 2 = 0,3 e log 3 = 0,4):

a) 1333
b) 2333
c) 3333
d) 4333
e) 5333

Questão 04. (UERJ) Exercícios sobre Função Exponencial: Pelos programas de controle de tuberculose, sabe-se que o risco de infecção R depende do tempo t, em anos, do seguinte modo: R = Ro ⋅ e^−kt , em que Ro é o risco de infecção no início da contagem do tempo t e k é o coeficiente de declínio. O risco de infecção atual em Salvador foi estimado em 2%. Suponha que, com a implantação de um programa nesta cidade, fosse obtida uma redução no risco de 10% ao ano, isto é, k = 10%.

Use a tabela abaixo para os cálculos necessários:

O tempo, em anos, para que o risco de infecção se torne igual a 0,2%, é de:
a) 21
b) 22
c) 23
d) 24

Questão 05. (UFF) Em um meio de cultura especial, a quantidade de bactérias, em bilhões, é dada pela função Q definida, para t ≥ 0, por Q(t) = k ⋅ 5^kt, sendo t o tempo, em minuto, e k uma constante.

A quantidade de bactérias, cuja contagem inicia-se com o cálculo de Q(0), torna-se, no quarto minuto, igual a 25 Q(0).

Assinale a opção que indica quantos bilhões de bactérias estão presentes nesse meio de cultura no oitavo minuto.
a) 12,5
b) 25
c) 312,5
d) 625
e) 1 000

Questão 06. (UFJF) A função c(t)=200 . 3^k.t, com k = 1/12, dá o crescimento do número C, de bactérias, no instante t em horas. O tempo necessário, em horas, para que haja, nessa cultura, 1 800 bactérias, está no intervalo:

a) [0, 4]
b) [4, 12]
c) [12, 36]
d) [36, 72]
e) [72, 108]

Questão 07. (PUC-Rio) Exercícios sobre Função Exponencial: Uma das soluções da equação = é:

a) x = 1
b) x = 0
c) x = 2
d) x = −2
e) x = 3

Questão 08. (M. Campos) Resolvendo as duas equações exponenciais 4^x-1 = e 3^2y+3  = 5^2y+3, obtém-se uma raiz para cada equação.

Nessas equações valor de x − y corresponde a:
a) 2,8
b) – 0,2
c) 0,8
d) 1

Questão 09. (UnB) A disseminação de uma doença infecciosa em uma determinada população de 30 000 frangos em uma granja pode ser descrita pela equação P(t) = , em que t é o número de dias decorridos desde a detecção da doença, que é definido como o momento do aparecimento dos primeiros casos – t = 0 – e P(t) é a quantidade total de frangos infectados após t dias. Com base nessas informações, julgue os itens a seguir, como verdadeiros (V) ou falsos (F).

( ) A quantidade de frangos infectados no momento em que a doença foi detectada é superior a 150.
( ) Caso a doença não seja controlada, toda a população de frangos da granja será infectada.
( ) 4 100 frangos serão infectados decorridos 2 +log 3 5 dias do momento da detecção da doença.
( ) O número de frangos infectados somente no terceiro dia é inferior a 1 200.

Questão 10. (Fatec) Exercícios sobre Função Exponencial: Se x é um número real tal que 2^-x . 4^x < 8^x+1, então:

a) – 2 < x < 2
b) x = 1
c) x = 0
d) x < 3/2
e) x > −3/2

>>> Confira nossa lista completa de exercícios sobre Matemática.

Gabarito com as respostas do simulado com Exercícios sobre Função Exponencial para Enem e Concurso:

01. B;

02. B;

03. A;

04. C;

05. C;

06. C;

07. A;

08. A;

09. F, F, V, F;

10. E

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína