Simulado sobre Inequações Exponenciais e Logarítmicas

Questão 01 sobre Inequações Exponenciais e Logarítmicas: (UFRS) A função f: IR → IR definida por f(x) = 2.b^x é exponencial crescente se, e somente se:
a) b > 0
b) b < 0
c) 0 < b < 1
d) b < 1
e) b > 1

Questão 02. (AFA) O conjunto-solução da inequação (0,5)^{x(x– 2)} < (0,25)^{x –1,5} é:

a) {x ∈ IR l x <1}.
b) {x ∈ IR l x >3}.
c) {x ∈ IR l 1 < x <3}.
d) {x ∈ IR l x < 1 ou x > 3}.

Questão 03 sobre Inequações Exponenciais e Logarítmicas: (UEL-PR) Quantos números inteiros e estritamente positivos são soluções da inequação 3^{x – 1} + 3^x  + 3^{x + 1} ≤ 39?

a) 0
b) 1
c) 2
d) 3
e) 4

Questão 04. (Fuvest) Se log10 x ≤ log24 . log4 6 . log6 8 – 1, então

a) 0 < x ≤ 10²
b) 102 < x ≤ 10⁴
c) 104 < x ≤ 10⁶
d) 106 < x ≤ 10⁸
e) x > 10⁸

Questão 05. (Mack) Na figura temos o esboço do gráfico de y = a^x + 1. O valor de 2^{3a – 2} é:

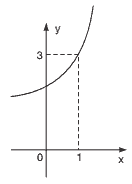
a) 16
b) 8
c) 2
d) 32
e) 64

Questão 06 sobre Inequações Exponenciais e Logarítmicas: (UFSCar) Para estimar a área da figura ABDO (sombreada no desenho), onde a curva AB é parte da representação gráfica da função f(x) = 2^x, João demarcou o retângulo OCBD e, em seguida, usou um programa de computador que “plota” pontos aleatoriamente no interior do retângulo a seguir:

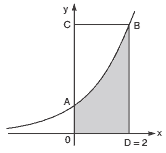
Sabendo que dos 1000 pontos “plotados”, apenas 540 ficaram no interior da figura ABDO, a área estimada dessa figura, em unidades de área, é igual a:
a) 4,32
b) 4,26
c) 3,92
d) 3,84
e) 3,52

🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.

Gabarito com as respostas do simulado com 06 exercícios de matemática sobre Inequações Exponenciais e Logarítmicas:

1) e;

2) d;

3) c;

4) a;

5) a;

6) a

Anderson Medeiros Dalbosco

Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína