Questão 01 sobre Cones: (UFC–2009) Ao seccionarmos um cone circular reto por um plano paralelo a sua base, cuja distância ao vértice do cone é igual a um terço da sua altura, obtemos dois sólidos: um cone circular reto S 1e um tronco de cone S2. A relação é igual a :
A) 33
B) 27
C) 26
D) 9
E) 3
Questão 02. (Mackenzie-SP) Planificando a superfície lateral de um cone, obtém-se o setor circular da figura, de centro O e raio 18 cm. Dos valores a seguir, o MAIS PRÓXIMO da altura desse cone é:
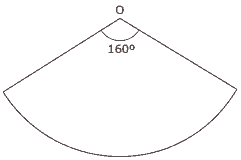
A) 12 cm.
B) 18 cm.
C) 14 cm.
D) 16 cm.
E) 20 cm.
Questão 03. (PUC-SP–2006) Considere o triângulo isósceles ABC, tal que AB = BC = 10 cm e CA = 12 cm. A rotação desse triângulo em torno de um eixo que contém o lado AB gera um sólido, cujo volume, em centímetros cúbicos, é:
A) 256π
B) 298,6π
C) 307,2π
D) 316π
E) 328,4π
Questão 04 sobre Cones: (UFOP-MG) Um reservatório de água com a forma de um cone circular reto tem 8 m de altura e, sua base, 3 m de raio. Se a água ocupa 40% da capacidade total do reservatório, o volume de água nele contido é:
A) 960π litros.
B) 4 800π litros.
C) 2 400π litros.
D) 9 600π litros.
E) 96 000π litros.
Questão 05. (UFSCar-SP) A figura representa um galheteiro para a colocação de azeite e vinagre em compartimentos diferentes, sendo um cone no interior de um cilindro.
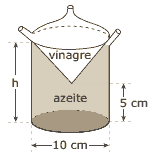
Considerando h como a altura máxima de líquido que o galheteiro comporta e a razão entre a capacidade total de azeite e vinagre igual a 5, o valor de h é:
A) 7 cm.
B) 8 cm.
C) 10 cm.
D) 12 cm.
E) 15 cm.
Questão 06. (UFPE) Um cone reto tem altura 12³2 cm e está cheio de sorvete. Dois amigos vão dividir o sorvete em duas partes de mesmo volume, usando um plano paralelo à base do cone.
Qual deverá ser a altura do cone menor assim obtido?
A) 12 cm
B) 12√2 cm
C) 12√3 cm
D) 10√2 cm
E) 10√3 cm
Questão 07 sobre Cones: (UFC) Um cone circular reto e uma pirâmide de base quadrada têm a mesma altura e o mesmo volume. Se r é a medida do raio da base do cone, e b é a medida do lado da base da pirâmide, então o quociente b r é igual a:
A)
B) 1
C)
D) p
E) 2π
Questão 08. (UFV-MG) Um chapéu, no formato de um cone circular reto, é feito de uma folha circular de raio 30 cm, recortando-se um setor circular de ângulo θ = radianos e juntando os lados.
A área da base do chapéu, em cm2, é:
A) 140π
B) 110π
C) 130π
D) 100π
E) 120π
Questão 09. (UFRRJ) Considerando um lustre de formato cônico com altura e raio da base igual a 0,25 m, a distância do chão H em que se deve pendurá-lo para obter um lugar iluminado em forma de círculo com área de 25π m2, é de:
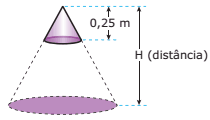
A) 12 m.
B) 10 m.
C) 8 m.
D) 6 m.
E) 5 m.
Questão 10 sobre Cones: (Enem–1999) Assim como na relação entre o perfil de um corte de um torno e a peça torneada, sólidos de revolução resultam da rotação de figuras planas em torno de um eixo. Girando-se as figuras a seguir em torno da haste indicada obtêm-se os sólidos de revolução que estão na coluna da direita.
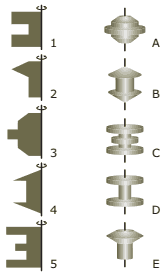
A correspondência correta entre as figuras planas e os sólidos de revolução obtidos é:
A) 1A, 2B, 3C, 4D, 5E.
B) 1B, 2C, 3D, 4E, 5A.
C) 1B, 2D, 3E, 4A, 5C.
D) 1D, 2E, 3A, 4B, 5C.
E) 1D, 2E, 3B, 4C, 5A.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da melhor lista de exercícios de matemática sobre Cones:
01. C;
02. D;
03. C;
04. D;
05. C;
06. A;
07. C;
08. D;
09. E;
10. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
