Questão 01 sobre Formas Trigonométricas: (UFSM-RS–2006) Dado z = x + yi, um número complexo, as soluções da equação |z – 2i| = 5 são representadas graficamente por:
A) uma reta que passa pela origem.
B) uma circunferência com centro (0, 2) e raio 5.
C) uma reta que passa por (0, 2).
D) uma circunferência com centro (2, 0) e raio 5.
E) uma reta que passa por (2, 0).
Questão 02. (UFU-MG) As representações gráficas dos números complexos z1= cos 30º + i.sen 30º e z2=cos102º+i.sen102º, no plano complexo, correspondem a vértices consecutivos de um polígono regular inscrito em uma circunferência com centro na origem.
O número de lados desse polígono é igual a:
A) 12
B) 6
C) 5
D) 10
Questão 03. (UEG–2006) O conjunto dos números complexos que satisfazem a condição |z – 3i| = |z – 2| é representado no plano cartesiano por uma reta:
A) cuja inclinação é positiva.
B) que contém a origem do sistema.
C) que não intercepta o eixo real.
D) cuja inclinação é negativa.
Questão 04 sobre Formas Trigonométricas: (Cesgranrio) O conjunto dos pontos z = x + yi do plano complexo que satisfazem |z – 1|2 = 2x e y ≥ 2 é:
A) o conjunto vazio.
B) uma região não limitada do plano.
C) todos os pontos x + yi tais que y ≥ 2.
D) uma reta.
E) diferente dos quatro anteriores.
Questão 05. (Mackenzie-SP) Seja t = 2 + 3i um número complexo. Se,
A = {z ∈ |z – t| ≤ 1}
B = {z ∈ |z = a + bi e b ≤ 3}
então, no plano de Argand-Gauss, A ∩ B é:
A) um conjunto vazio.
B) uma semicircunferência.
C) um semicírculo.
D) uma circunferência.
E) um círculo.
Questão 06. (Cesgranrio) No plano complexo, o conjunto dos pontos z = x + yi, tais que |z| ≤ 1 e y ≥ 0, é:
A) uma circunferência.
B) um círculo.
C) um quadrado centrado na origem.
D) um semicírculo.
E) um segmento de reta.
Questão 07 sobre Formas Trigonométricas: (PUC Minas) A forma trigonométrica do número complexo y = 4√3 + 4i é:
A) 8.(cos 30° + i.sen 30°)
B) 8.(cos 45° + i.sen 45°)
C) 8.(cos 60° + i.sen 60°)
D) 8.(cos 120° + i.sen 120°)
E) 8.(cos 150° + i.sen 150°)
Questão 08. (UEBA) Na figura a seguir, o ponto P é o afixo do número complexo z.
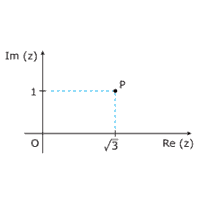
A forma trigonométrica de z2 é:
A) 4.(cos 15° + i.sen 15°)
B) 4.(cos 60° + i.sen 60°)
C) 2.(cos 60° + i.sen 60°)
D) 2.(cos 30° + i.sen 30°)
E) cos 15° + i.sen 15°
Questão 09. (UEL-PR) Sejam z1 e z2 os números complexos z1 = 3.(cos 30° + i.sen 30°) e z2 = 5.(cos 45° + i.sen 45°). O produto de z1 por z2 é o número complexo:
A) 15.(cos 1 350° + i.sen 1 350°)
B) 8.(cos 75º + i.sen 75°)
C) 8.(cos 1 350º + i.sen 1 350°)
D) 15.(cos 15º + i.sen 15°)
E) 15.(cos 75º + i.sen 75°)
Questão 10 sobre Formas Trigonométricas: (FUVEST-SP) Dado o número complexo z = √3 + i, qual é o MENOR valor do inteiro n ≥ 1 para o qual zn é um número real?
A) 2
B) 4
C) 6
D) 8
E) 10
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista de exercícios de Matemática sobre Formas Trigonométricas:
01. B;
02. C;
03. A;
04. A;
05. C;
06. D;
07. A;
08. B;
09. E;
10. C
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
