Questão 01 sobre Pirâmides Matemáticas: (UFOP) A aresta lateral de uma pirâmide quadrangular regular mede 10 m e a altura, 8 m. Encontre seu volume.
Questão 02. (UFF) A grande pirâmide de Quéops, antiga construção localizada no Egito é uma pirâmide regular de base quadrada, com 137 m de altura. Cada face dessa pirâmide é um triângulo isósceles cuja altura relativa à base mede 179 m. A área da base da pirâmide, em m2, é:
a) 13.272.
b) 26.544
c) 39.816
d) 53.088
e) 79.432
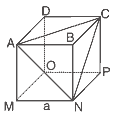
Questão 03. (PUC – SP) No cubo abaixo, faz-se um corte pelo plano que passa pelos vértices A, C e N, retirando-se o sólido ABCN assim obtido. Determine o volume do sólido restante em função de a, sabendo que a é a medida do lado.
Questão 04 sobre Pirâmides Matemáticas: Calcule o volume da pirâmide triangular regular de aresta lateral 13 cm e cuja base está inscrita num círculo de área 25πcm2.
Questão 05. (UFSM 2015) Desde a descoberta do primeiro plástico sintético da história, esse material vem sendo aperfeiçoado e aplicado na indústria. Isso se deve ao fato de o plástico ser leve, ter alta resistência e flexibilidade. Uma peça plástica usada na fabricação de um brinquedo tem a forma de uma pirâmide regular quadrangular em que o apótema mede 10 mm e a aresta da base mede 12 mm. A peça possui para encaixe, em seu interior, uma parte oca de volume igual a 78 mm3 O volume, em mm3, dessa peça é igual a:
a) 1152.
b) 1074.
c) 402.
d) 384.
e) 306.
Questão 06. (UEPB 2013) A altura de um tetraedro regular que possui área total e volume numericamente iguais, é:
a) 2 √6
b) 36
c) 6
d) 6 √2
e) 12
Questão 07 sobre Pirâmides Matemáticas: (UEPG 2013) Uma pirâmide quadrangular regular tem 36 cm2 de área da base. Sabendo que a altura da pirâmide tem 3 √3cm, assinale o que for correto.
01) A área lateral da pirâmide é o dobro da área da base.
02) A área total da pirâmide é o triplo da área da base.
04) A área de uma face lateral da pirâmide é a sexta parte de sua área total.
08) A razão das áreas total e lateral dessa pirâmide é um número fracionário.
16) O volume dessa pirâmide é 108 √3cm3
Questão 08. (Ufrgs 2012) Se duplicarmos a medida da aresta da base de uma pirâmide quadrangular regular e reduzirmos sua altura à metade, o volume desta pirâmide:
a) será reduzido à quarta parte.
b) será reduzido à metade.
c) permanecerá inalterado.
d) será duplicado.
e) aumentará quatro vezes.
Questão 09. (Insper 2012) Em uma pirâmide quadrangular regular, a área lateral é o dobro da área da base. Nesse caso, cada face lateral forma com o plano da base um ângulo que mede:
a) 15°.
b) 30°.
c) 45°.
d) 60°.
e) 75°.
Questão 10. A base de uma pirâmide hexagonal regular está inscrita em um círculo de raio 6 3 cm. Assim, a medida, em cm2, da área da base dessa pirâmide é:
a) 27 √3 .
b) 36 √3 .
c) 45 √3 .
d) 55 √3 .
e) 81 v3 .
Questão 11 sobre Pirâmides Matemáticas: (Unesp 2011) Há 4.500 anos, o Imperador Quéops do Egito mandou construir uma pirâmide regular que seria usada como seu túmulo.
As características e dimensões aproximadas dessa pirâmide hoje, são:
1ª) Sua base é um quadrado com 220 metros de lado;
2ª) Sua altura é de 140 metros.
Suponha que, para construir parte da pirâmide equivalente a 1,88 × 104 m3, o número médio de operários utilizados como mão de obra gastava em média 60 dias. Dados que:
2,22 × 1,4 ≅ 6,78 e 2,26 ÷ 1,88 ≅ 1,2
e mantidas estas médias, o tempo necessário para a construção de toda pirâmide, medido em anos de 360 dias, foi de, aproximadamente:
a) 20.
b) 30.
c) 40.
d) 50.
e) 60.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista de Exercícios sobre Pirâmides Matemáticas:
01) 192 m3 ;
02) d; 3)5a3/6;
04) V = 75 √3cm3;
05) e;
06) e;
07) 01 + 02 + 04 + 08 = 15;
08) d;
09) d;
10) a;
11) a
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
