Questão 01. (UFU-MG–2007) Exercícios sobre Probabilidade: De uma urna que contém bolas numeradas de 1 a 100 será retirada uma bola. Sabendo-se que qualquer uma das bolas tem a mesma chance de ser retirada, qual é a probabilidade de se retirar uma bola cujo número é um quadrado perfeito ou um cubo perfeito?
A) 0,14 B) 0,1 C) 0,12 D) 0,16
Questão 02. (UFOP-MG–2008) Em um laboratório, existem n substâncias. Sabe-se que exatamente duas dessas substâncias não podem estar simultaneamente em qualquer mistura, porque provocam explosão. Um aluno que desconhece esse fato resolve misturar 6 das n substâncias. Sendo a probabilidade de explosão na mistura feita pelo aluno de 1 para 14, DETERMINE o número n de substâncias existentes no laboratório.
Questão 03. (Enem–2006) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o prêmio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas casas. Na discussão para se decidir com quem ficaria o troféu, travou-se o seguinte diálogo: Pedro, camisa 6: — Tive uma ideia. Nós somos 11 jogadores e nossas camisas estão numeradas de 2 a 12. Tenho dois dados com as faces numeradas de 1 a 6. Se eu jogar os dois dados, a soma dos números das faces que ficarem para cima pode variar de 2 (1 + 1) até 12 (6 + 6). Vamos jogar os dados, e quem tiver a camisa com o número do resultado vai guardar a taça. Tadeu, camisa 2: — Não sei não… Pedro sempre foi muito esperto… Acho que ele está levando alguma vantagem nessa proposta… Ricardo, camisa 12: — Pensando bem… Você pode estar certo, pois, conhecendo o Pedro, é capaz que ele tenha mais chances de ganhar que nós dois juntos… Desse diálogo, conclui-se que:
A) Tadeu e Ricardo estavam equivocados, pois a probabilidade de ganhar a guarda da taça era a mesma para todos.
B) Tadeu tinha razão e Ricardo estava equivocado, pois, juntos, tinham mais chances de ganhar a guarda da taça do que Pedro.
C) Tadeu tinha razão e Ricardo estava equivocado, pois, juntos, tinham a mesma chance que Pedro de ganhar a guarda da taça.
D) Tadeu e Ricardo tinham razão, pois os dois juntos tinham menos chances de ganhar a guarda da taça do que Pedro.
E) Não é possível saber qual dos jogadores tinha razão, por se tratar de um resultado probabilístico, que depende exclusivamente da sorte.
Questão 04. (UFPE–2009) Exercícios sobre Probabilidade: Escolhendo aleatoriamente um dos anagramas da palavra COVEST, qual a probabilidade de suas primeira e última letras serem consoantes?
a) b) c) d) e)
Questão 05. (UFU-MG–2008) Lança-se um dado não viciado e se observa o número correspondente à face que caiu voltada para cima.
Sejam a, b e c, respectivamente, os valores observados em três lançamentos sucessivos. Se x = a.102 + b.10 + c, então a probabilidade de esse número x de três algarismos ser divisível por 2 ou por 5 é igual a: a) b) c) d)
Instrução: Texto para as questões 06 e 07. Em um concurso de televisão, apresentam-se ao participante 3 fichas voltadas para baixo, estando representada em cada uma delas as letras T, V e E. As fichas encontram-se alinhadas em uma ordem qualquer. O participante deve ordenar as fichas ao seu gosto, mantendo as letras voltadas para baixo, tentando obter a sigla TVE. Ao desvirá-las, para cada letra que esteja na posição correta ganhará um prêmio de R$ 200,00.
Questão 06. (Enem–1998) A probabilidade de o participante não ganhar qualquer prêmio é igual a:
a) 0 b) c) d) e)
Questão 07. (Enem–1998) Exercícios sobre Probabilidade: A probabilidade de o concorrente ganhar exatamente o valor de R$ 400,00 é igual a:
a) 0 b) c) d) e)
Questão 08. (Enem–2006) A tabela a seguir indica a posição relativa de quatro times de futebol na classificação geral de um torneio, em dois anos consecutivos. O símbolo ● significa que o time indicado na linha ficou, no ano de 2004, à frente do indicado na coluna. O símbolo * significa que o time indicado na linha ficou, no ano de 2005, à frente do indicado na coluna.
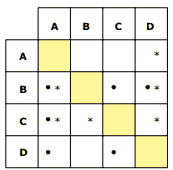
A probabilidade de que um desses quatro times, escolhido ao acaso, tenha obtido a mesma classificação no torneio, em 2004 e 2005, é igual a: A) 0,00 B) 0,25 C) 0,50 D) 0,75 E) 1,00
Questão 09. (Enem–2009) A população brasileira sabe, pelo menos intuitivamente, que a probabilidade de acertar as seis dezenas da Mega Sena não é zero, mas é quase. Mesmo assim, milhões de pessoas são atraídas por essa loteria, especialmente quando o prêmio se acumula em valores altos. Até junho de 2009, cada aposta de seis dezenas, pertencentes ao conjunto {01, 02, 03, …, 59, 60}, custava R$ 1,50. Disponível em: <www.caixa.gov.br>. Acesso em: 7 jul. 2009.
Considere que uma pessoa decida apostar exatamente R$ 126,00 e que esteja mais interessada em acertar apenas cinco das seis dezenas da Mega Sena, justamente pela dificuldade desta última. Nesse caso, é melhor que essa pessoa faça 84 apostas de seis dezenas diferentes, que não tenham cinco números em comum, do que uma única aposta com nove dezenas, porque a probabilidade de acertar a quina no segundo caso em relação ao primeiro é, aproximadamente,
a) 1 vezes menor b) 2 vezes menor C) 4 vezes menor D) 9 vezes menor E) 14 vezes menor
Questão 10. (UFG–2007) Exercícios sobre Probabilidade: Um grupo de 150 pessoas é formado por 28% de crianças, enquanto o restante é composto de adultos. Classificando esse grupo por sexo, sabe-se que entre os de sexo masculino é formado por crianças e que entre os de sexo feminino também é formado por crianças. Escolhendo ao acaso uma pessoa nesse grupo, CALCULE a probabilidade de essa pessoa ser uma criança do sexo feminino.
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
