Questão 01 sobre Binômio de Newton e Triângulo de Pascal: (UFOP-MG) Para que se tenha um dos termos do desenvolvimento de (x + a)11 igual a 1 386×5, o valor de a deve ser:
a)
b)
c) √10
d) 3
e) 3√10
Questão 02. (PUC Rio) O coeficiente de x no desenvolvimento é:
A) 10
B) 35
C) 15
D) 6
E) 20
Questão 03. (FGV-SP) Se , então n é igual a:
A) 4
B) 6
C) 9
D) 5
E) 8
Questão 04 sobre Binômio de Newton e Triângulo de Pascal: (UFSM-RS) O coeficiente de x5 no desenvolvimento de é dado por:
A) 0
B) 1
C) 8
D) 28
E) 56
Questão 05. (PUC Rio) No desenvolvimento do binômio o termo independente de x é o:
A) 1º
B) 3º
C) 2º
D) 5º
E) 4º
Questão 06. (UFP I) Se a e b são números reais tais que (a + b)10 = 1 024 e se o 6º termo do desenvolvimento binomial é igual a 252, então:
a) a = e b =
b) a = 3 e b = -1
c) a = e b =
d) a = e b =
e) a = 1 e b = 1
Questão 07 sobre Binômio de Newton e Triângulo de Pascal: (UFBA) Sabendo-se que a soma dos coeficientes no desenvolvimento do binômio (a + b)m é igual a 256, CALCULE :
Questão 08. (UFV-MG) A soma dos coeficientes do desenvolvimento de (2x + 3y)m é 625. O valor de m é:
A) 5
B) 6
C) 10
D) 3
E) 4
Questão 09. (PUC RS) Se o terceiro termo do desenvolvimento de (a + b)n é 21.a5.b2, então o sexto termo é:
A) 35.a4.b3
B) 21.a3.b4
C) 21.a2.b5
D) 7.a.b6
E) 7.a2.b5
Questão 10. (Mackenzie-SP) No desenvolvimento , t ∈ N, os coeficientes binominais do quarto e do décimo terceiro termos são iguais. Então, o termo independente de x é o:
A) décimo.
B) décimo primeiro.
C) nono.
D) décimo segundo.
E) oitavo.
Questão 11. (PUC Rio) Se (1 + x + x2)n = A0 + A1x + A2x2 + … + A2nx2n, então A0 + A1 + A2 + … + A2n vale:
a) 2n-1
b) 3n
c)
d)
e)
Questão 12 sobre Binômio de Newton e Triângulo de Pascal: (Cesgranrio) O valor de n na igualdade = 254 é:
A) 6
B) 7
C) 8
D) 9
E) 10
Questão 13. (Mackenzie-SP) Os 3 primeiros coeficientes no desenvolvimento de estão em progressão aritmética. O valor de n é:
A) 4
B) 6
C) 8
D) 10
E) 12
Questão 14. (Mackenzie-SP) O coeficiente do termo em x–3 no desenvolvimento de é:
A) 1
B) 6
C) 10
D) 15
E) inexistente.
Questão 15 sobre Binômio de Newton e Triângulo de Pascal: (UFOP-MG–2010) Considere a função f: A → B definida como f(x) = C6, x, em que A = {0, 1, 2, 3, 4, 5, 6}, B é um subconjunto de (conjunto dos números inteiros positivos sem o zero) e C6, x representa a combinação simples de 6 elementos de A tomados x a x. Veja a seguir o gráfico dessa função.
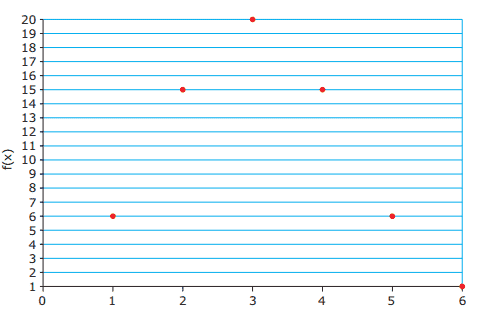
Uma aplicação do cálculo combinatório é o desenvolvimento da potência n-ésima do Binômio de Newton. A fórmula do Binômio de Newton é expressa por:
(a + b)n = Cn,x an-x bx
Com base nessas informações, avalie os itens seguintes e, posteriormente, marque a alternativa VERDADEIRA.
I. O número de elementos do conjunto domínio de f é inferior ao número de elementos do conjunto imagem de f.
II. C6, 1 + C6, 2 < C6, 3 + C6, 6
III. (1 + h)3 > 1 + C 3, 0 + C3, 1 h + C3, 2 h2 + C3, 3h3
IV. (r + h)6 = r6 + 6r5h + 15r4h2 + 20r3h3 + 15r2h4 + 6rh5 + h6
A) Todos os itens estão incorretos.
B) Existem três itens incorretos e um correto.
C) Existem três itens corretos e um incorreto.
D) Todos os itens estão corretos.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas do simulado com 15 exercícios de matemática sobre Binômio de Newton e Triângulo de Pascal:
01. A;
02. B;
03. E;
04. C;
05. D;
06. E;
07. 24;
08. E;
09. C;
10. B;
11. B;
12. C;
13. C;
14. D;
15. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
