Questão 01 sobre Área de Triângulo e Equação Geral da Reta: (Ufam) O triângulo ABC, de vértices A(-1, -2), B(1, -2) e C(1,m), tem área igual a 10, então m é:
a) – 8 ou – 12
b) 8 ou – 12
c) 6 ou 10
d) – 6 ou – 10
e) 6 ou – 10
Questão 02. (UFP) Determine a área do triângulo cujas coordenadas são A(3, 11), B(-9, -5) e C(6, -10):
a) 180
b) 150
c) 120
d) 100
e) 80
Questão 03. (Ita 2000) A área de um triângulo é de 4 unidades de superfície, sendo dois de seus vértices os pontos A(2, 1) e B(3, -2).
Sabendo que o terceiro vértice encontra-se sobre o eixo das abcissas, pode-se afirmar que suas coordenadas são:
a) (-1/2, 0) ou (5, 0).
b) (-1/2, 0) ou (4, 0).
c) (-1/3, 0) ou (5, 0).
d) (-1/3, 0) ou (4, 0).
e) (-1/5, 0) ou (3, 0).
Questão 04 sobre Área de Triângulo e Equação Geral da Reta: (Fatec) As retas r e s interceptam o eixo das abcissas nos pontos A e B e são concorrentes no ponto P.
Se suas equações são 3x – y +1 = 0 e 2x + y – 4 = 0, então a área do triângulo ABP é:
a) 7/10
b) 7/3
c) 27/10
d) 49/15
e) 28/5
Questão 05. (Imed 2016) Dadas as equações das retas r: x – 2y – 10 = 0 e s: 3x + 2y – 6 = 0 e representadas no mesmo sistema de coordenadas cartesianas, pode-se afirmar que a abscissa do ponto de intersecção entre as retas r e s é:
a) – 3.
b) – 2.
c) 2.
d) 4.
e) 6.
Questão 06. (Ifsul 2015) Observe a figura abaixo onde estão representadas algumas ruas de Pelotas.

Considere que:
1. As larguras das ruas sejam desprezíveis e o lado de cada quadra seja 01 (uma) unidade de medida;
2. Todas as quadras sejam quadradas de dimensões iguais;
3. A rua Gomes Carneiro seja o EIXO DAS ABSCISSAS;
4. A rua XV de Novembro seja o EIXO DAS ORDENADAS;
5. O cruzamento das ruas Tiradentes e Mal. Deodoro seja o PONTO A;
6. O cruzamento das ruas Alm. Tamandaré e Gonçalves Chaves seja o PONTO B.
A equação da reta que passa pelos pontos A e B é:
a) x + y + 1 = 0
b) x + y – 1 = 0
c) x – y – 1 = 0
d) x – y + 1 = 0
Questão 07. (Uerj 2016) Na região conhecida como Triângulo das Bermudas, localizada no oceano Atlântico, é possível formar um triângulo com um vértice sobre a cidade porto-riquenha de San Juan, outro sobre a cidade estadunidense de Miami e o terceiro sobre as ilhas Bermudas.
A figura abaixo mostra um sistema de coordenadas cartesianas ortogonais, com os vértices do triângulo devidamente representados. A escala utilizada é 1:17.000.000, e cada unidade nos eixos cartesianos equivale ao comprimento de 1 cm.
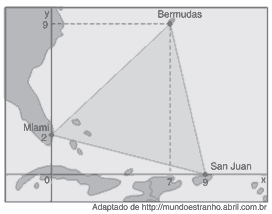
Calcule, em km2, a área do Triângulo das Bermudas, conforme a representação plana da figura.
Questão 08 sobre Área de Triângulo e Equação Geral da Reta: (PUC – RJ 2015) Sejam r e s as retas de equações x – y – 2 = 0 e x + 2y – 5 = 0 respectivamente, representadas no gráfico abaixo. Seja A o ponto de interseção das retas r e s. Sejam B e C os pontos de interseção de r e s com o eixo horizontal, respectivamente.
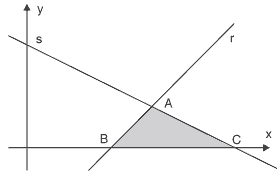
A área do triângulo ABC vale:
a) 1,0
b) 1,5
c) 3,0
d) 4,5
e) 6,0
Questão 09. (UFC) Considere o triângulo cujos vértices são os pontos A(2, 0); B(0, 4) e C(2 , 4 + √5 ). Determine o valor numérico da altura relativa ao lado AB, deste triângulo.
Questão 10 sobre Área de Triângulo e Equação Geral da Reta: Modelo Enem. A área do quadrilátero ABCD de vértices A(4,2), B(8,4), C(9,9) e D(1,5) é:
a) 21
b) 22
c) 25
d) 27
e) 30
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da lista com 10 Exercícios de Matemática sobre Área de Triângulo e Equação Geral da Reta:
01. b;
02. b;
03. c;
04. d;
05. d;
06. b ;
07. Área = 1.112.650 km2
08. b;
09. 5;
10. d
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
