Questão 01 sobre Pirâmides e Cones: Unifor-CE – Um triângulo retângulo é tal que as medidas de seus lados, em centímetros, são numericamente iguais aos termos de uma progressão aritmética de razão 1,5. Girando-se esse triângulo em torno do cateto menor obtém-se um sólido cujo volume, em centímetros cúbicos, é:
a) 40,5π
b) 45π
c) 48π
d) 52,5π
e) 54π
Questão 02. UFMS – Considerando as perdas de material ocorridas na fabricação de um único copo, o fabricante concluiu corretamente que:
a) A opção 1 é mais econômica, pois as perdas são 25% menores que na opção 2.
b) A opção 2 é mais econômica, pois as perdas são 50% menores que na opção 1.
c) As duas opções são equivalentes, pois as perdas são as mesmas.
d) A opção 2 é mais econômica, pois as perdas são 25% menores que na opção 1.
e) A opção 1 é mais econômica, pois as perdas são 50% menores que na opção 2.
Questão 03. UFMS – Levando em consideração que as dimensões das folhas a serem divididas em quadrados são de 1,25 m x 2,15 m, o fabricante calculou que, se escolher a opção 1, o número de copinhos que pode confeccionar com uma única folha é igual a:
a) 228
b) 252
c) 210
d) 268
e) 196
Questão 04 sobre Pirâmides e Cones: UFMS – Para conferir a adequação da produção às suas especificações, um comprador calculou que a capacidade do copinho projetado era, aproximadamente, em mL de:
a) 120
b) 90
c) 150
d) 60
e) 30
Questão 05. U. Católica-DF – Um reservatório em forma de cone circular reto, de eixo vertical, com altura igual a 4 cm e raio da base igual a 3 cm, está completamente cheio de água. Uma esfera é colocada no cone até se apoiar na parede do mesmo, de modo que os centros da esfera e da base do cone coincidam.
O volume de água, em cm3, que transborda do cone é:
a) menor que 24;
b) maior que 24 e menor que 26;
c) maior que 26 e menor que 28;
d) maior que 28 e menor que 30;
e) maior que 30.
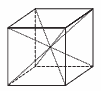
Questão 06. UFPE – Na figura abaixo o cubo de aresta medindo 6 está dividido em pirâmides congruentes de bases quadradas e com vértices no centro do cubo. Qual o volume de cada pirâmide?
a) 36
b) 48
c) 54
d) 64
e) 72
Questão 07 sobre Pirâmides e Cones: U. Potiguar-RN – O raio da base de um cone é 15 cm e a altura 4 cm. Aumentando-se a altura e diminuindo-se o raio da base do cone, de uma medida x cm com x ≠ 0, para obter-se outro cone circular reto, de mesmo volume que o original, qual deve ser o valor de x?
a) 4 cm
b) 5 cm
c) 10 cm
d) 9 cm
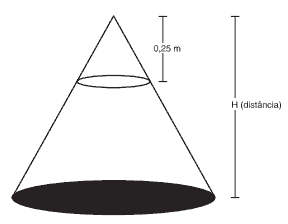
Questão 08. UFR-RJ – Considerando um lustre de formato cônico com altura e raio da base igual a 0,25 m, a distância do chão (H) em que se deve pendurá-lo para obter um lugar iluminado em forma de círculo com área de 25π m2, é de:
a) 12 m
b) 10 m
c) 8 m
d) 6 m
e) 5 m
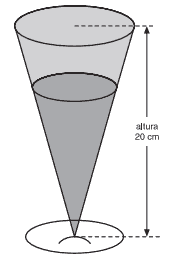
Questão 09. UFMT – Uma casa de sucos naturais utiliza copos da forma tulipa (conforme figura abaixo), que possuem volume de 300 mL e altura interna de 20 cm. Calcule a altura do líquido, em centímetros, medida a partir do fundo, quando um cliente deixa sobrar no copo 37,5 mL.
Observação: Suponha que a superfície interna do copo seja cônica circular.
Questão 10 sobre Pirâmides e Cones: PUC-RS – Um cilindro circular reto e um cone circular reto têm o mesmo raio da base, medindo 3 m, e a mesma altura, medindo 4 m. A razão entre as áreas laterais do cilindro e do cone é:
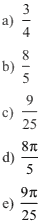
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas das atividades de Matemática sobre Pirâmides e Cones:
01. E;
02. C;
03. B;
04. D;
05. E;
06. A;
07. B;
08. E;
09. 10;
10. B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
