Questão 01 sobre Propriedades da P. G.: (PUC Rio–2007) A sequência 10x, 10x + 1, 10x + 2, … representa:
A) uma progressão aritmética de razão 10.
B) uma progressão aritmética de razão 1.
C) uma progressão geométrica de razão 10.
D) uma progressão geométrica de razão 1.
E) nem progressão aritmética nem progressão geométrica.
Questão 02. (UEL-PR–2007) Para testar o efeito da ingestão de uma fruta rica em determinada vitamina, foram dados pedaços dessa fruta a macacos. As doses da fruta são arranjadas em uma sequência geométrica, sendo 2 g e 5 g as duas primeiras doses.
Qual a alternativa CORRETA para continuar essa sequência?
A) 7,5 g; 10,0 g; 12,5 g …
B) 125 g; 312 g; 619 g …
C) 8 g; 11 g; 14 g …
D) 6,5 g; 8,0 g; 9,5 g …
E) 12,500 g; 31,250 g; 78,125 g …
Questão 03. (UFU-MG) Sejam a1, a2, a3 números reais cuja soma é igual a 88. Sabendo-se que a1 – 2, a2, a3 estão, nessa ordem, em progressão geométrica de razão 6, determine o maior desses números.
A) 6
B) 12
C) 72
D) 24
E) 32
Questão 04 sobre Propriedades da P. G.: (FGV-SP–2010) Um capital de R$ 1 000,00 é aplicado a juro simples, à taxa de 10% ao ano; os montantes, daqui a 1, 2, 3, …, n anos, formam a sequência (a1, a2, a3, …, an). Outro capital de R$ 2 000,00 é aplicado a juro composto, à taxa de 10% ao ano gerando a sequência de montantes (b1, b2, b3, …, bn) daqui a 1, 2, 3, …, n anos. As sequências (a1, a2, a3, …, an) e (b1, b2, b3, …, bn) formam, respectivamente:
A) uma progressão aritmética de razão 1,1 e uma progressão geométrica de razão 10%.
B) uma progressão aritmética de razão 100 e uma progressão geométrica de razão 0,1.
C) uma progressão aritmética de razão 10% e uma progressão geométrica de razão 1,10.
D) uma progressão aritmética de razão 1,10 e uma progressão geométrica de razão 1,10.
E) uma progressão aritmética de razão 100 e uma progressão geométrica de razão 1,10.
Questão 05. (UEL-PR–2007) Um automóvel zero km é comprado por R$ 32 000,00. Ao final de cada ano, seu valor diminui 10% em função da depreciação do bem.
O valor APROXIMADO do automóvel, após seis anos, é de:
A) R$ 15 006,00.
B) R$ 19 006,00.
C) R$ 16 006,00.
D) R$ 12 800,00.
E) R$ 17 006,00.
Questão 06. (PUC Minas–2006) O número de assinantes de uma revista de circulação na grande BH aumentou, nos quatro primeiros meses de 2005, em progressão geométrica, conforme assinalado na tabela a seguir:

Com base nessas informações, pode-se afirmar que, de fevereiro para abril, o número de assinantes dessa revista teve um aumento igual a:
A) 1 050
B) 1 155
C) 1 510
D) 1 600
Questão 07 sobre Propriedades da P. G.: (PUC Minas–2007) Depois de percorrer um comprimento de arco de 12 m, uma criança deixa de empurrar o balanço em que está brincando. Se o atrito diminui a velocidade do balanço de modo que o comprimento de arco percorrido seja sempre igual a 80% do anterior, a distância total percorrida pela criança, em metros, até que o balanço pare completamente, é dada pela expressão D = 12 + 0,80.12 + 0,80.(0,80.12) + … .
Observando-se que o segundo membro dessa igualdade é a soma dos termos de uma progressão geométrica, pode-se estimar que o valor de D, em metros, é igual a:
A) 24
B) 36
C) 48
D) 60
Questão 08. (UFSM-RS) A sequência de números reais (x, y, z, t) forma, nessa ordem, uma progressão aritmética cuja soma dos termos é 160; a sequência de números reais (x, y, w, u) forma, nessa ordem, uma progressão geométrica de razão 3. Assim, a soma t + u é:
A) 440
B) 340
C) 240
D) 140
E) 40
Questão 09. (Enem–2008) Fractal (do latim fractus, fração, quebrado) – objeto que pode ser dividido em partes que possuem semelhança com o objeto inicial. A geometria fractal, criada no século XX, estuda as propriedades e o comportamento dos fractais – objetos geométricos formados por repetições de padrões similares.
O Triângulo de Sierpinski, uma das formas elementares da geometria fractal, pode ser obtido por meio dos seguintes passos:
1. Comece com um triângulo equilátero (figura 1).
2. Construa um triângulo em que cada lado tenha a metade do tamanho do lado do triângulo anterior e faça três cópias.
3. Posicione essas cópias de maneira que cada triângulo tenha um vértice comum com um dos vértices de cada um dos outros dois triângulos, conforme ilustra a figura 2.
4. Repita sucessivamente os passos 2 e 3 para cada cópia dos triângulos obtidos no passo 3 (figura 3).
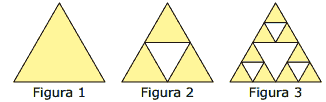
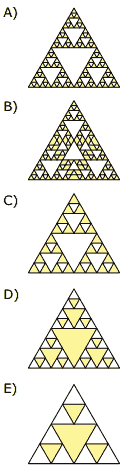
De acordo com o procedimento descrito, a figura 4 da sequência apresentada anteriormente é:
Questão 10 sobre Propriedades da P. G.: Modelo Enem. Nascido em 1845, o matemático russo Georg Cantor teve um papel extremamente importante no desenvolvimento da Matemática Moderna, particularmente na elaboração da Teoria dos Conjuntos. Um outro trabalho de Cantor é o chamado Conjunto de Cantor, que é representado a seguir:

A montagem desse conjunto é feita do seguinte modo:
• Toma-se um segmento de reta (1ª linha);
• Divide-se esse segmento em três partes iguais, suprimindo-se a parte central (2ª linha);
• Repete-se o processo em cada segmento de reta remanescente (3ª linha), e assim por diante.
Repetindo-se esse processo indefinidamente, o número de segmentos de reta presentes na 10ª linha é igual a:
A) 64
B) 128
C) 256
D) 512
E) 1 024
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas da melhor lista de exercícios de Matemática sobre Propriedades da P. G.:
01. C;
02. E;
03. C;
04. E;
05. E;
06. B;
07. D;
08. B;
09. C;
10. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
