Questão 01 sobre Progressão Geométrica: Modelo Enem. Desejo ter, para minha aposentadoria, 1 milhão de reais. Para isso, faço uma aplicação financeira, que rende 1% de juros ao mês, já descontados o imposto de renda e as taxas bancárias recorrentes. Se desejo me aposentar após 30 anos com aplicações mensais fixas e ininterruptas nesse investimento, o valor aproximado, em reais, que devo disponibilizar mensalmente é:
Dado: 1,01361 ≈ 36
a) 290,00.
b) 286,00.
c) 282,00.
d) 278,00.
e) 274,00.
Questão 02. Modelo Enem. Considere o padrão de construção representado pelos desenhos a seguir.
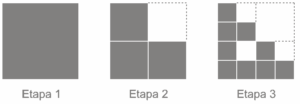
Na Etapa 1, há um único quadrado com lado 10. Na Etapa 2, esse quadrado foi dividido em quatro quadrados congruentes, sendo um deles retirado, como indica a figura. Na etapa 3 e nas seguintes, o mesmo processo é repetido em cada um dos quadrados da etapa anterior. Nessas condições, a área restante na Etapa 6 será de:
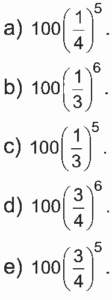
Questão 03. Modelo Enem. No início de janeiro de 2004, Fábio montou uma página na internet sobre questões de vestibulares. No ano de 2004, houve 756 visitas à página.
Supondo que o número de visitas à página, durante o ano, dobrou a cada bimestre, o número de visitas à página de Fábio no primeiro bimestre de 2004 foi
a) 36.
b) 24.
c) 18.
d) 16.
e) 12.
Questão 04 sobre Progressão Geométrica: Modelo Enem. No dia 10 de dezembro, uma pessoa enviou pela internet uma mensagem para x pessoas. No dia 2, cada uma das x pessoas que recebeu a mensagem no dia 10 enviou a mesma para outras duas novas pessoas. No dia 3, cada pessoa que recebeu a mensagem no dia 2 também enviou a mesma para outras duas novas pessoas.
E, assim, sucessivamente. Se, do dia 10 até o final do dia 6 de dezembro, 756 pessoas haviam recebido a mensagem, o valor de x é:
a) 12.
b) 24.
c) 52.
d) 63.
e) 126.
Questão 05. Modelo Enem. Considere as sequências (an) e (bn) definidas por:
an+1 = 2n e bn+1 = 3n, n ≥ 0.
Então, o valor de a11.b6 é
a) 211 . 36.
b) (12)5.
c) 515.
d) 615.
e) 630.
Questão 06. Modelo enem. A sequência de números reais a, b, c, d forma, nessa ordem, uma progressão aritmética cuja soma dos termos é 110; a sequência de números reais a, b, e, f forma, nessa ordem, uma progressão geométrica de razão 2. A soma d + f é igual a:
a) 96.
b) 102.
c) 120.
d) 132.
e) 142.
Questão 07. Modelo enem. Os comprimentos das circunferências de uma sequência de círculos concêntricos formam uma progressão aritmética de razão 2. Os raios desses círculos formam uma:
a) progressão geométrica de razão 1/2.
b) progressão geométrica de razão 1/ð.
c) progressão aritmética de razão 2.
d) progressão aritmética de razão ð.
e) progressão aritmética de razão 1/π.
Questão 08 sobre Progressão Geométrica: Modelo enem. Nascido em 1845, o matemático russo Georg Cantor teve um papel extremamente importante no desenvolvimento da Matemática Moderna, particularmente na elaboração da Teoria dos Conjuntos. Um outro trabalho de Cantor é o chamado Conjunto de Cantor, que é representado a seguir:

A montagem desse conjunto é feita do seguinte modo:
• Toma-se um segmento de reta (1ª linha);
• Divide-se esse segmento em três partes iguais, suprimindo-se a parte central (2ª linha);
• Repete-se o processo em cada segmento de reta remanescente (3ª linha), e assim por diante.
Repetindo-se esse processo indefinidamente, o número de segmentos de reta presentes na 10ª linha é igual a:
A) 64
B) 128
C) 256
D) 512
E) 1 024
Questão 09. (Enem–2008) Fractal (do latim fractus, fração, quebrado) – objeto que pode ser dividido em partes que possuem semelhança com o objeto inicial. A geometria fractal, criada no século XX, estuda as propriedades e o comportamento dos fractais – objetos geométricos formados por repetições de padrões similares.
O Triângulo de Sierpinski, uma das formas elementares da geometria fractal, pode ser obtido por meio dos seguintes passos:
1. Comece com um triângulo equilátero (figura 1).
2. Construa um triângulo em que cada lado tenha a metade do tamanho do lado do triângulo anterior e faça três cópias.
3. Posicione essas cópias de maneira que cada triângulo tenha um vértice comum com um dos vértices de cada um dos outros dois triângulos, conforme ilustra a figura 2.
4. Repita sucessivamente os passos 2 e 3 para cada cópia dos triângulos obtidos no passo 3 (figura 3).
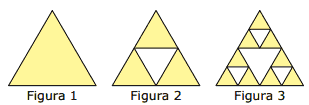
De acordo com o procedimento descrito, a figura 4 da sequência apresentada anteriormente é:
a) 
b) 
c) 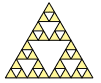
d) 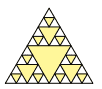
e) 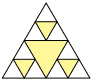
Questão 10 sobre Progressão Geométrica: (UFSM-RS) No piso do hall de entrada de um shopping, foi desenhado um quadrado Q1 de 10 m de lado, no qual está inscrito um segundo quadrado Q2 obtido da união dos pontos médios dos lados do quadrado anterior, e assim sucessivamente, Q3, Q4, …, formando uma sequência infinita de quadrados, seguindo a figura. Dessa forma, a soma das áreas dos quadrados é de:
A) 25 m2.
B) 25√2 m2.
C) 200 m2.
D) 50√2 m2.
E) 100(2 + √2) m2.
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas dos exercícios de matemática sobre Progressão Geométrica:
01. B;
02. E;
03. E;
04. A;
05. E;
06. D;
07. E;
08. D;
09. C;
10. C
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
