Questão 01. (UEL-PR) Exercícios sobre Proporções: Sabe-se que a sequência (x, y, z) é inversamente proporcional à sequência . Se x + y + z = 176, então x – y é igual a:
A)
B)
C) 2z
D) 4z
E) 6z
Questão 02. (PUC-Campinas-SP) Segundo a Lei de Boyle-Mariotte, sabe-se que “a uma temperatura constante, os volumes de uma mesma massa de gás estão na razão inversa das pressões que produzem”. Se, sob a pressão de 5 atmosferas, uma massa de gás ocupa um volume de 0,6 dm3, a expressão que permite calcular a pressão p, em atmosferas, em função do volume v, em dm3, ocupado por essa massa de gás, é:
A) V =
B) V = 3P
C) V =
D) V =
E) V =
Questão 03. (Enem–2009) O Indicador do CadÚnico (ICadÚnico), que compõe o cálculo do Índice de Gestão Descentralizada do Programa Bolsa Família (IGD), é obtido por meio da média aritmética entre a taxa de cobertura qualificada de cadastros (TC) e a taxa de atualização de cadastros (TA), em que , NV é o número de cadastros domiciliares válidos no perfil do CadÚnico, NF é o número de famílias estimadas como público-alvo do CadÚnico e NA é o número de cadastros domiciliares atualizados no perfil do CadÚnico.
Portaria n° 148, 27 de abr. 2006 (Adaptação).
Suponha que o IcadÚnico de um município específico é 0,6. Porém, dobrando NF o IcadÚnico cairá para 0,5. Se NA + NV = 3 600, então NF é igual a:
A) 10 000
B) 7 500
C) 5 000
D) 4 500
E) 3 000
Questão 04. (Enem–2009) Exercícios sobre Proporções: Segundo as regras da Fórmula 1, o peso mínimo do carro, de tanque vazio, com o piloto, é de 605 kg, e a gasolina deve ter densidade entre 725 e 780 gramas por litro. Entre os circuitos nos quais ocorrem competições dessa categoria, o mais longo é Spa-Francorchamps, na Bélgica, cujo traçado tem 7 km de extensão. O consumo médio de um carro da Fórmula 1 é de 75 litros para cada 100 km. Suponha que um piloto de uma equipe específica, que utiliza um tipo de gasolina com densidade de 750 g/L, esteja no circuito de Spa-Francorchamps, parado no box para reabastecimento.
Caso ele pretenda dar mais 16 voltas, ao ser liberado para retornar à pista, seu carro deverá pesar, no mínimo:
A) 617 kg.
B) 668 kg.
C) 680 kg.
D) 689 kg.
E) 717 kg.
Questão 05. (UFPE) Uma substância X é composta de três elementos A, B e C, na proporção de 2:3:5 partes de volume. Um litro do elemento A pesa três vezes mais que um litro do elemento C, enquanto um litro do elemento B pesa duas vezes mais que um litro do elemento C. Se x é o quociente entre o peso de um litro da substância X e o peso de um litro do elemento C, DETERMINE x.
Questão 06. (Unicamp-SP) Dois navios partiram ao mesmo tempo, de um mesmo porto, em direções perpendiculares e a velocidades constantes. Trinta minutos após a partida, a distância entre os dois navios era de 15 km e, após mais 15 minutos, um dos navios estava 4,5 km mais longe do porto que o outro.
A) Quais as velocidades dos dois navios, em km/h?
B) Qual a distância de cada um dos navios até o porto de saída, 270 minutos após a partida?
Questão 07. (Enem–2010) Exercícios sobre Proporções: A resistência elétrica e as dimensões do condutor
A relação da resistência elétrica com as dimensões do condutor foi estudada por um grupo de cientistas por meio de vários experimentos de eletricidade. Eles verificaram que existe proporcionalidade entre:
• resistência (R) e comprimento (l), dada a mesma secção transversal (A);
• resistência (R) e área da secção transversal (A), dado o mesmo comprimento (l) e
• comprimento (l) e área da secção transversal (A), dada a mesma resistência (R).
Considerando os resistores como fios, pode-se exemplificar o estudo das grandezas que influem na resistência elétrica utilizando as figuras seguintes.
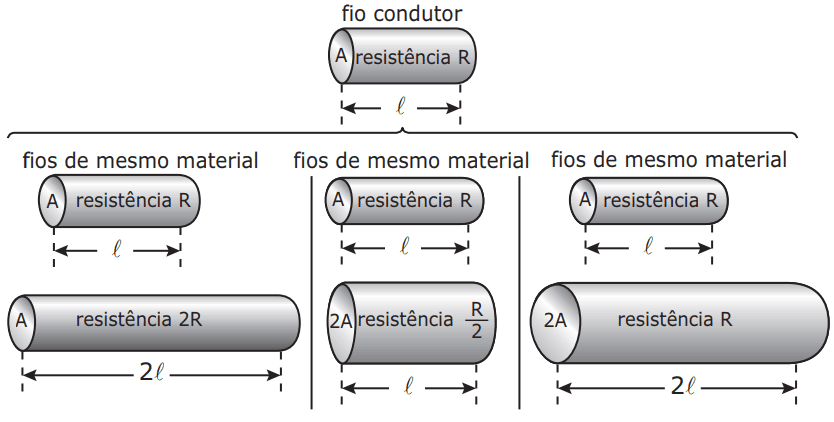
Disponível em: <http://www.efeitojoule.com>. Acesso em: abr. 2010 (Adaptação).
As figuras mostram que as proporcionalidades existentes entre resistência (R) e comprimento (l), resistência (R) e área da secção transversal (A), e entre comprimento (l) e área da secção transversal (A) são, respectivamente:
A) direta, direta e direta.
B) direta, direta e inversa.
C) direta, inversa e direta.
D) inversa, direta e direta.
E) inversa, direta e inversa.
Questão 08. (Unicamp-SP) Retiraram-se x litros de vinho de um barril de 100 litros e adicionaram-se, ao mesmo barril, x litros de água. Da mistura resultante no barril, retiram-se outros x litros e adicionam-se outros x litros de água.
Agora o barril contém 64 litros de vinho e 36 de água. CALCULE o valor de x.
Questão 09. (Mackenzie-SP) Na figura a seguir, Q é um ponto do gráfico da função y = f(x), com x e y inversamente proporcionais.
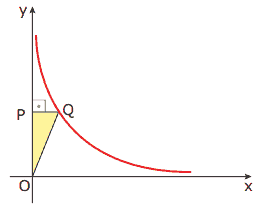
Se (x, y) = é um ponto da curva, então a área do triângulo OPQ é:
A) 160
B) 320
C) 380
D) 400
E) 800
>>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as resposta do simulado com Exercícios sobre Proporções:
01. E;
02. A;
03. C;
04. B;
05. x = 1,7;
06. A) 24 km/h e 18 km/h
B) 108 km e 81 km;
07. C;
08. x = 20;
09. D
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
